题目内容
若函数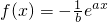 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是
- A.在圆外
- B.在圆内
- C.在圆上
- D.不能确定
B
分析:求出f(x)的导函数,把x等于0代入导函数即可求出切线的斜率,然后把x等于0代入f(x)求出切点的纵坐标,根据切点坐标和斜率写出直线l的方程,由题意可知直线l与圆相离,得到圆心到直线的距离大于圆的半径,利用点到直线的距离公式求出圆心到直线l的距离d,让d大于圆的半径得到一个关系式,化简得到a2+b2<1,即可得到点P与圆的位置关系.
解答: ,∴
,∴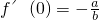 .
.
又∵切点为(0,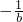 ),
),
∴切线l的方程为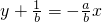 ,即ax+by+1=0.
,即ax+by+1=0.
∴圆心C(0,0)到直线l的距离 .
.
∴a2+b2<1.
∴P(a,b)在圆C:x2+y2=1内.
故选B.
点评:此题考查学生会利用导数求曲线上过某点切线的斜率,灵活运用点到直线的距离公式及两点间的距离公式化简求值,掌握直线与圆的位置关系及点与圆的位置关系所满足的条件,是一道多知识的综合题.
分析:求出f(x)的导函数,把x等于0代入导函数即可求出切线的斜率,然后把x等于0代入f(x)求出切点的纵坐标,根据切点坐标和斜率写出直线l的方程,由题意可知直线l与圆相离,得到圆心到直线的距离大于圆的半径,利用点到直线的距离公式求出圆心到直线l的距离d,让d大于圆的半径得到一个关系式,化简得到a2+b2<1,即可得到点P与圆的位置关系.
解答:
 ,∴
,∴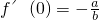 .
.又∵切点为(0,
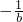 ),
),∴切线l的方程为
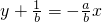 ,即ax+by+1=0.
,即ax+by+1=0.∴圆心C(0,0)到直线l的距离
 .
.∴a2+b2<1.
∴P(a,b)在圆C:x2+y2=1内.
故选B.
点评:此题考查学生会利用导数求曲线上过某点切线的斜率,灵活运用点到直线的距离公式及两点间的距离公式化简求值,掌握直线与圆的位置关系及点与圆的位置关系所满足的条件,是一道多知识的综合题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的图象在x=0处的切线
的图象在x=0处的切线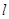 与圆
与圆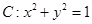 相离,则
相离,则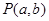 与圆C的位置关系是( )
与圆C的位置关系是( )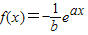 的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .
的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .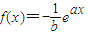 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )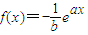 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )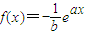 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )