题目内容
已知动点P对应的复数z满足|z+c|+|z-c|=2a(a>c>0),且点P与点A(-a,0),B(a,0)连线的斜率之积为-
,则
等于( )
| 1 |
| 2 |
| c |
| a |
A.
| B.
| C.
| D.
|
∵动点P对应的复数z满足|z+c|+|z-c|=2a(a>c>0),
∴动点P的轨迹为复平面内的椭圆:
+
=1.
设P(x0,y0),则
+
=1 ①,
由点P与点A(-a,0),B(a,0)连线的斜率之积为-
,得
•
=-
②,
联立①②得:a2=2b2,
又b2=a2-c2,
∴a2=2(a2-c2),
解得:
=
.
故选:B.
∴动点P的轨迹为复平面内的椭圆:
| x2 |
| a2 |
| y2 |
| b2 |
设P(x0,y0),则
| x02 |
| a2 |
| y02 |
| b2 |
由点P与点A(-a,0),B(a,0)连线的斜率之积为-
| 1 |
| 2 |
| y0 |
| x0+a |
| y0 |
| x0-a |
| 1 |
| 2 |
联立①②得:a2=2b2,
又b2=a2-c2,
∴a2=2(a2-c2),
解得:
| c |
| a |
| ||
| 2 |
故选:B.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
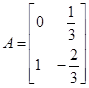 ,点
,点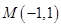 ,
,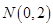 .求线段
.求线段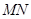 在矩阵
在矩阵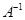 对应的变换作用下得到线段
对应的变换作用下得到线段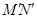 的长度.
的长度.