题目内容
(本小题满分12分)已知函数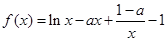
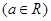 .
.
(Ⅰ)当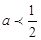 时,讨论
时,讨论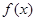 的单调性;
的单调性;
(Ⅱ)当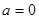 时,对于任意的
时,对于任意的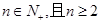 ,证明:不等式
,证明:不等式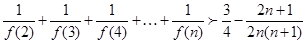
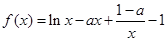
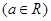 .
.(Ⅰ)当
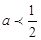 时,讨论
时,讨论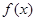 的单调性;
的单调性;
(Ⅱ)当
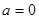 时,对于任意的
时,对于任意的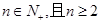 ,证明:不等式
,证明:不等式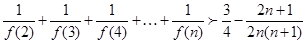
(I)原函数的定义域为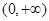 ,因为
,因为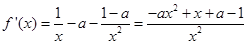
当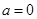 时,
时,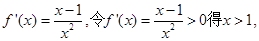 所以此时函数
所以此时函数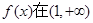 上是增函数,在
上是增函数,在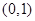 上是减函数;
上是减函数;
当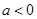 时,令
时,令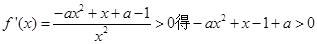 ,解得
,解得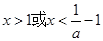 (舍去),此时函数
(舍去),此时函数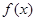 在
在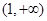 上增函数,在
上增函数,在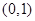 上是减函数;根据
上是减函数;根据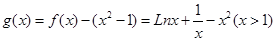 的单调性,变形得得
的单调性,变形得得
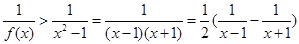 ,令
,令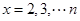 证得。
证得。
当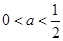 时,令
时,令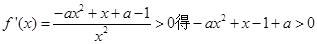 ,解得
,解得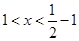
此时函数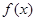 在
在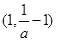 上是增函数,在
上是增函数,在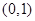 和
和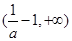 上是减函数 ………6分
上是减函数 ………6分
(II)由(I)知: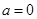 时,
时,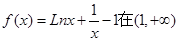 上是增函数,
上是增函数,
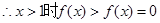
设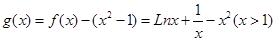
则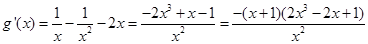
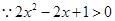 恒成立
恒成立 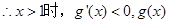 单调递减
单调递减
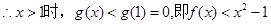
又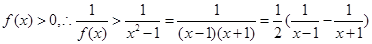
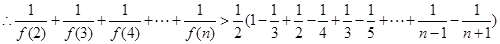
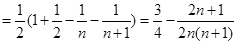
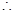 不等式得证 …………………………………12分
不等式得证 …………………………………12分
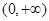 ,因为
,因为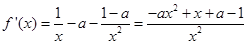
当
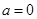 时,
时,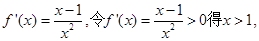 所以此时函数
所以此时函数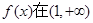 上是增函数,在
上是增函数,在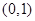 上是减函数;
上是减函数;当
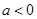 时,令
时,令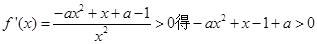 ,解得
,解得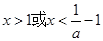 (舍去),此时函数
(舍去),此时函数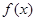 在
在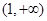 上增函数,在
上增函数,在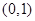 上是减函数;根据
上是减函数;根据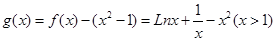 的单调性,变形得得
的单调性,变形得得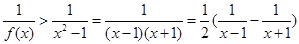 ,令
,令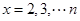 证得。
证得。当
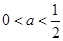 时,令
时,令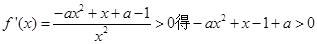 ,解得
,解得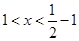
此时函数
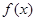 在
在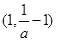 上是增函数,在
上是增函数,在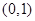 和
和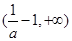 上是减函数 ………6分
上是减函数 ………6分(II)由(I)知:
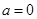 时,
时,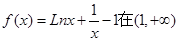 上是增函数,
上是增函数,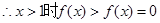
设
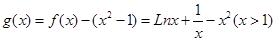
则
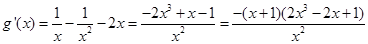
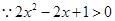 恒成立
恒成立 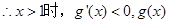 单调递减
单调递减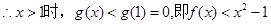
又
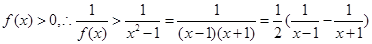
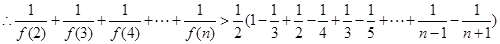
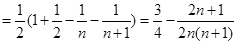
 不等式得证 …………………………………12分
不等式得证 …………………………………12分(Ⅰ)求导函数,讨论a对单调性的影响;

练习册系列答案
相关题目
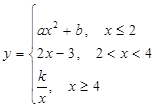 的图象如图所示.
的图象如图所示.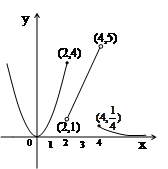
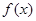 的定义域为
的定义域为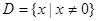 ,且满足对于任意
,且满足对于任意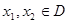 ,有
,有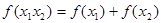 .
.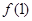 的值;
的值;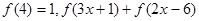 ≤
≤ ,且
,且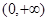 上是增函数,求
上是增函数,求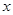 的取值范围.
的取值范围.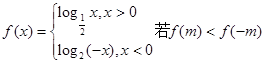 ,则实数m的取值范围是()
,则实数m的取值范围是()



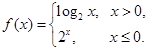 若
若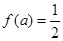 ,则
,则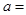 ( )
( )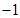
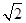
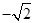
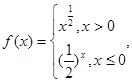 则
则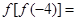 ( )
( )


 若
若 ,则实数a = ( )
,则实数a = ( )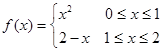 的图像与x轴所围成的封闭图形的面积为 .
的图像与x轴所围成的封闭图形的面积为 .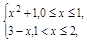 则
则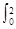 f(x)dx=
f(x)dx=