题目内容
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足 ,
, •
• =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E.(1)求曲线E的方程;
(2)过点S(0,
 )且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足
)且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足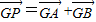 使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.
使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.
【答案】分析:(1)先判断NP为AM的中垂线,从而可得|CN|+|AN|=2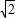 ,故可知动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,由此可得曲线E的方程;
,故可知动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,由此可得曲线E的方程;
(2)动直线l的方程为:y=kx- 与椭圆方程联立,消元可得(2k2+1)x2-
与椭圆方程联立,消元可得(2k2+1)x2- kx-
kx-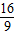 =0,假设在y上存在定点G(0,m),使得以AB为直径的圆恒过这个点,则
=0,假设在y上存在定点G(0,m),使得以AB为直径的圆恒过这个点,则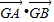 =0恒成立,故可得点G的坐标,进而可得四边形NAPB面积,利用基本不等式,可确定最值.
=0恒成立,故可得点G的坐标,进而可得四边形NAPB面积,利用基本不等式,可确定最值.
解答:解:(1)∵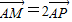 ,
,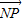 •
•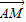 =0,
=0,
∴NP为AM的垂直平分线,∴|NA|=|NM|.
又∵|CN|+|NM|=2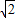
∴|CN|+|AN|=2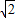 >2
>2
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为2a=2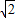 ,焦距2c=2
,焦距2c=2
∴a=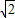 ,c=1,∴b2=1
,c=1,∴b2=1
∴曲线E的方程为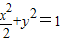 ;
;
(2)动直线l的方程为:y=kx- 与椭圆方程联立,消元可得(2k2+1)x2-
与椭圆方程联立,消元可得(2k2+1)x2- kx-
kx-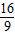 =0
=0
设A(x1,y1),B(x2,y2),则 ,
,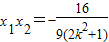
假设在y上存在定点G(0,m),满足题设,则 =(x1,y1-m),
=(x1,y1-m), =(x2,y2-m),
=(x2,y2-m),
∴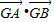 =x1x2+(y1-m)(y2-m)=
=x1x2+(y1-m)(y2-m)=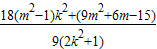
由假设得对于任意的k∈R,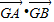 =0恒成立,∴m2-1=0且9m2+m-15-0,解得m=1.
=0恒成立,∴m2-1=0且9m2+m-15-0,解得m=1.
因此,在y轴上存在定点G,使得以AB为直径的圆恒过这个点,点G的坐标为(0,1)
这时,点G到AB的距离d=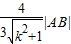 =
=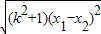
SGAPB=|AB|d=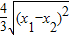 =
=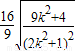
设2k2+1=t,则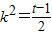 ,得t∈[1,+∞),
,得t∈[1,+∞),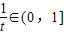
所以SGAPB=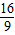
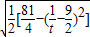 ≤
≤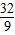 ,当且仅当
,当且仅当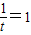 时,上式等号成立.
时,上式等号成立.
因此,四边形NAPB面积的最大值是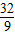 .
.
点评:本题是直线与圆锥曲线的综合问题的考查,是综合题有一定的难度,考查利用圆锥曲线的定义求曲线方程,考查直线与椭圆的位置关系,考查面积的计算,考查基本不等式的运用,属于中档题.
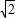 ,故可知动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,由此可得曲线E的方程;
,故可知动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,由此可得曲线E的方程;(2)动直线l的方程为:y=kx-
 与椭圆方程联立,消元可得(2k2+1)x2-
与椭圆方程联立,消元可得(2k2+1)x2- kx-
kx-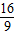 =0,假设在y上存在定点G(0,m),使得以AB为直径的圆恒过这个点,则
=0,假设在y上存在定点G(0,m),使得以AB为直径的圆恒过这个点,则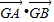 =0恒成立,故可得点G的坐标,进而可得四边形NAPB面积,利用基本不等式,可确定最值.
=0恒成立,故可得点G的坐标,进而可得四边形NAPB面积,利用基本不等式,可确定最值.解答:解:(1)∵
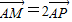 ,
,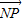 •
•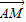 =0,
=0,∴NP为AM的垂直平分线,∴|NA|=|NM|.
又∵|CN|+|NM|=2
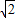
∴|CN|+|AN|=2
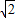 >2
>2∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为2a=2
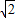 ,焦距2c=2
,焦距2c=2∴a=
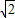 ,c=1,∴b2=1
,c=1,∴b2=1∴曲线E的方程为
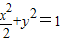 ;
;(2)动直线l的方程为:y=kx-
 与椭圆方程联立,消元可得(2k2+1)x2-
与椭圆方程联立,消元可得(2k2+1)x2- kx-
kx-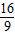 =0
=0设A(x1,y1),B(x2,y2),则
 ,
,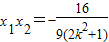
假设在y上存在定点G(0,m),满足题设,则
 =(x1,y1-m),
=(x1,y1-m),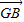 =(x2,y2-m),
=(x2,y2-m),∴
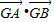 =x1x2+(y1-m)(y2-m)=
=x1x2+(y1-m)(y2-m)=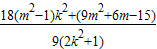
由假设得对于任意的k∈R,
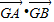 =0恒成立,∴m2-1=0且9m2+m-15-0,解得m=1.
=0恒成立,∴m2-1=0且9m2+m-15-0,解得m=1.因此,在y轴上存在定点G,使得以AB为直径的圆恒过这个点,点G的坐标为(0,1)
这时,点G到AB的距离d=
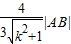 =
=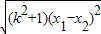
SGAPB=|AB|d=
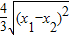 =
=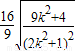
设2k2+1=t,则
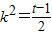 ,得t∈[1,+∞),
,得t∈[1,+∞),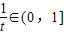
所以SGAPB=
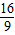
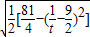 ≤
≤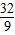 ,当且仅当
,当且仅当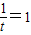 时,上式等号成立.
时,上式等号成立.因此,四边形NAPB面积的最大值是
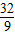 .
.点评:本题是直线与圆锥曲线的综合问题的考查,是综合题有一定的难度,考查利用圆锥曲线的定义求曲线方程,考查直线与椭圆的位置关系,考查面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足 (理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ,
,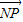 •
• =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E. )且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足
)且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足 使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.
使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.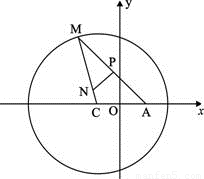
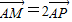 ,
, •
• =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E. )且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足
)且斜率为k的动直线l交曲线E于A、B两点,在y轴上是否存在定点G,满足 使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.
使四边形NAPB为矩形?若存在,求出G的坐标和四边形NAPB面积的最大值;若不存在,说明理由.