题目内容
已知M、N是正四面体PABC的棱AB、PC的中点.求:(1)异面直线PM、BN所成角的大小;
(2)BN与底面ABC所成角的大小;
(3)相邻两侧面所成的角.
解析:(1)设正四面体PABC的棱长为a,连结MC,取其中点R,连结NR和BR,易证PM∥NR,故∠BNR就是异面直线PM、BN所成的角,?
NR=![]() PM=
PM=![]() a,BN=
a,BN=![]() a,?
a,?
BR=![]() .?
.?
由余弦定理cos∠BNR=![]() ,?
,?
∴∠BNR=arccos![]() .?
.?
(2)作NH⊥MC于H,PG⊥MC于G,则∠NBH即为BN与底面ABC所成的角,由上可知G是△ABC的中心,?
∴GM=![]() MC=
MC=![]() a.?
a.?
∴PG=![]() ?
?
=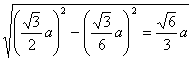 ,?
,?
sin∠NBH=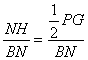 ?
?
=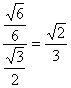 ,?
,?
即∠NBH=arcsin![]() .?
.?
(3)∠PMC即为相邻两面所成的角,∠PMC=arccos![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目