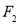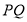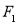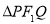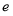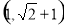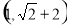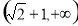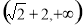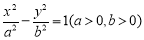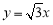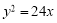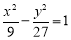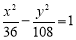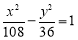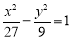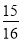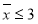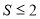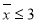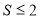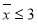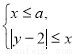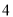题目内容
已知椭圆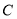 :
: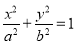
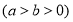 的离心率
的离心率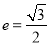 ,原点到过点
,原点到过点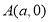 ,
,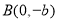 的直线的距离是
的直线的距离是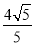 .
.
(1)求椭圆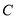 的方程;
的方程;
(2)若椭圆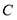 上一动点
上一动点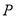
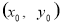 关于直线
关于直线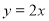 的对称点为
的对称点为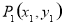 ,求
,求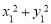 的取值范围;
的取值范围;
(3)如果直线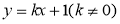 交椭圆
交椭圆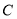 于不同的两点
于不同的两点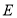 ,
,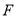 ,且
,且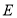 ,
,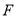 都在以
都在以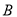 为圆心的圆上,求
为圆心的圆上,求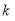 的值.
的值.
(1)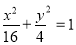 (2)
(2)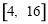 (3)
(3)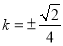
【解析】
试题分析:(1)由截距式可得直线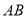 的方程,根据点到线的距离公式可得
的方程,根据点到线的距离公式可得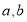 间的关系,又因为
间的关系,又因为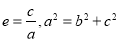 ,解方程组可得
,解方程组可得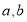 的值。(2)由点关于直线的对称点问题可知直线
的值。(2)由点关于直线的对称点问题可知直线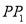 和直线
和直线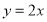 垂直,且
垂直,且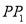 的中点在直线
的中点在直线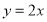 上,由此可用
上,由此可用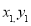 表示出
表示出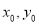 。再将点
。再将点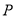 代入椭圆方程将
代入椭圆方程将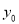 用
用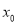 表示代入上式,根据椭圆方程可的
表示代入上式,根据椭圆方程可的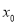 的范围,从而可得出所求范围。(3)将直线
的范围,从而可得出所求范围。(3)将直线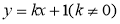 和椭圆方程联立,消去
和椭圆方程联立,消去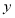 得关于
得关于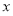 的一元二次方程,根据韦达定理可得根与系数的关系。根据题意可知
的一元二次方程,根据韦达定理可得根与系数的关系。根据题意可知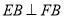 ,可根据斜率相乘等于
,可根据斜率相乘等于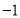 列出方程,也可转化为向量数量积为0列出方程。
列出方程,也可转化为向量数量积为0列出方程。
试题解析:(Ⅰ)因为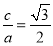 ,
,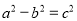 ,所以
,所以 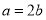 .
.
因为原点到直线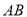 :
: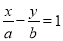 的距离
的距离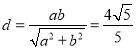 ,解得
,解得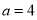 ,
,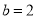 .
.
故所求椭圆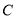 的方程为
的方程为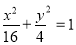 . 4分
. 4分
(Ⅱ)因为点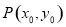 关于直线
关于直线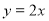 的对称点为
的对称点为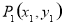 ,
,
所以  解得
解得 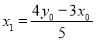 ,
,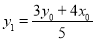 .
.
所以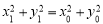 .
.
因为点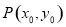 在椭圆
在椭圆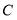 :
: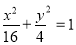 上,所以
上,所以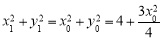 .
.
因为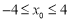 , 所以
, 所以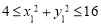 .所以
.所以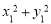 的取值范围为
的取值范围为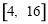 . 9分
. 9分
(Ⅲ)由题意 消去
消去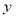 ,整理得
,整理得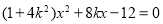 .可知
.可知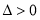 .
.
设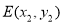 ,
,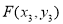 ,
,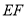 的中点是
的中点是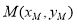 ,
,
则 ,
,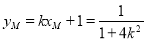 .
.
所以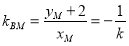 . 所以
. 所以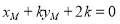 .
.
即 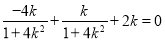 . 又因为
. 又因为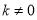 ,
,
所以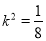 .
.
所以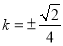 14分
14分
考点:1点到线的距离; 2椭圆方程;3点关于线的对称点;4转换思想。

练习册系列答案
相关题目