题目内容
已知非负实数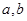
满足
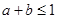,则关于
的一元二次方程
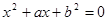有实根的概率是（ ）
A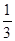． | B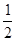． | C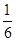． | D． |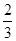
A
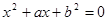解析试题分析：关于的一元二次方程有实根，则
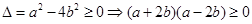，又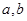为非负实数，所以
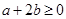，从而
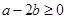.由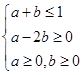
作出平面区域：
由图知，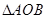
表示非负实数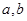满足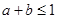的平面区域；
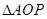表示其中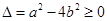
的平面区域. 又
，
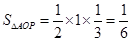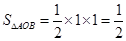.所以所求概率为
.
考点：平面区域、几何概型
练习册系列答案
相关题目
设变量
满足约束条件
，则
的最小值为（ ）
A． | B． | C． | D． |
设实数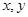
满足约束条件
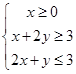，则
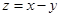的最小值为 ( )
A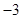． | B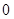． | C． | D． |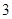
已知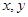
满足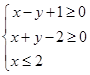
，则目标函数
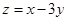的最小值是( )
A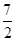． | B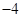． | C． | D． |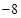
若实数
、
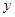满足条件
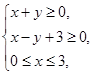则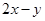
的最大值为（ ）
A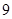． | B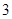． | C． | D． |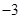
设m＞1，在约束条件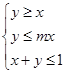
下，目标函数z＝x＋my的最大值小于2，则m的取值范围为( )
A．(1，1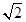＋ ) | B．(1+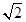，＋∞) | C．(1，3) | D．(3，＋∞) |
若实数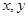
满足不等式组
，则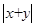
的最小值为（ ）
| A．3 | B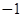． | C．1 | D．2 |
已知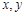
满足
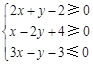，则关于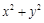
的说法，正确的是（ ）
| A．有最小值1 | B．有最小值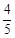 | C．有最大值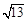 | D．有最小值 |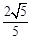
已知实数x，y满足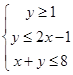
，则目标函数z＝x－y的最小值为( )
| A．－2 | B．5 | C．6 | D．7 |