题目内容
若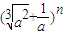 的展开式中含a3项,则最小自然数n是 .
的展开式中含a3项,则最小自然数n是 .
【答案】分析:根据 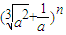 的展开式的通项公式为 Tr+1=Cnr
的展开式的通项公式为 Tr+1=Cnr 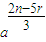 ,令
,令 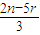 =3,n=
=3,n=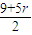 ,r=0,1,2,3,…n,故最小的n=
,r=0,1,2,3,…n,故最小的n=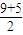 =7.
=7.
解答:解: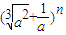 的展开式的通项公式为 Tr+1=Cnr
的展开式的通项公式为 Tr+1=Cnr 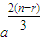 a-r=Cnr
a-r=Cnr 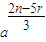 ,
,
令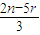 =3,n=
=3,n=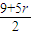 ,∴9+5r 为偶数,r=0,1,2,3,…n,
,∴9+5r 为偶数,r=0,1,2,3,…n,
故最小的n=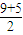 =7,
=7,
故答案为7.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,得到 n=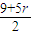 ,是解题的关键.
,是解题的关键.
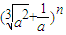 的展开式的通项公式为 Tr+1=Cnr
的展开式的通项公式为 Tr+1=Cnr 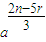 ,令
,令 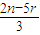 =3,n=
=3,n=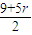 ,r=0,1,2,3,…n,故最小的n=
,r=0,1,2,3,…n,故最小的n=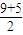 =7.
=7.解答:解:
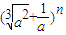 的展开式的通项公式为 Tr+1=Cnr
的展开式的通项公式为 Tr+1=Cnr 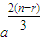 a-r=Cnr
a-r=Cnr 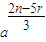 ,
,令
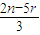 =3,n=
=3,n=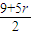 ,∴9+5r 为偶数,r=0,1,2,3,…n,
,∴9+5r 为偶数,r=0,1,2,3,…n,故最小的n=
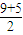 =7,
=7,故答案为7.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,得到 n=
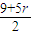 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
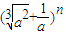 的展开式中含a3项,则最小自然数n是 .
的展开式中含a3项,则最小自然数n是 .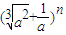 的展开式中含a3项,则最小自然数n是 .
的展开式中含a3项,则最小自然数n是 .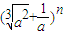 的展开式中含a3项,则最小自然数n是 .
的展开式中含a3项,则最小自然数n是 . 的展开式中含a3项,则最小自然数n是 .
的展开式中含a3项,则最小自然数n是 .