题目内容
实验表明,某型号的汽车每小时的耗油量y(升)与速度x(千米/小时)的关系式为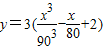 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时.(1)当车速度x(千米/小时)时,从甲地到乙地的耗油量为f(x)(升),求函数f(x)的解析式并指出函数的定义域;
(2)当车速为多大时,从甲地到乙地的耗油量最少?
【答案】分析:(1)由已知中每小时的耗油量y(升)与速度x(千米/小时)的关系式,甲乙两地相距180千米,则当车速度x(千米/小时)时,花费的时间为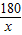 小时,进而得到函数f(x)的解析式,结合甲乙两地相距180千米,可得到函数的定义域;
小时,进而得到函数f(x)的解析式,结合甲乙两地相距180千米,可得到函数的定义域;
(2)根据(1)中得到的函数解析式,求出导函数的表达式,结合根据导数法求函数最值的方法和步骤,我们易确定出车速为多大时,从甲地到乙地的耗油量最少.
解答:解:(1)∵每小时的耗油量y(升)与速度x(千米/小时)的关系式为 ,
,
甲乙两地相距180千米,当车速度x(千米/小时)时,
f(x)=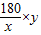 =
=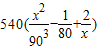 ,x∈(0,V]…6分(2)∵f(x)=
,x∈(0,V]…6分(2)∵f(x)=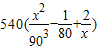 ,
,
∴f′(x)=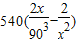
令f′(x)=0,解得x=90…8分
若V<90,有f′(x)<0,则函数f(x)在区间(0,V)内为单调减函数,所以车速为V(千米/小时)时,从甲地到乙地的耗油量最小;…11分
若V≥90,当0<x<90时,f′(x)<0;当90<x≤V时,f′(x)>0,所以,当x=90时,f(x)最小.…14分
综上:若V<90,车速为V(千米/小时)时,从甲地到乙地的耗油量最小;若V≥90,车速为90(千米/小时)时,从甲地到乙地的耗油量最小.…15
点评:本题考查的知识点是函数模型的选择与应用,利用导数求闭区间上的函数的最值,其中在建立函数模型时,由实际出发分析自变量的取值范围(定义域)是应用题的易忽略点,而(2)中要注意对V的取值进行分类讨论.
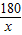 小时,进而得到函数f(x)的解析式,结合甲乙两地相距180千米,可得到函数的定义域;
小时,进而得到函数f(x)的解析式,结合甲乙两地相距180千米,可得到函数的定义域;(2)根据(1)中得到的函数解析式,求出导函数的表达式,结合根据导数法求函数最值的方法和步骤,我们易确定出车速为多大时,从甲地到乙地的耗油量最少.
解答:解:(1)∵每小时的耗油量y(升)与速度x(千米/小时)的关系式为
 ,
,甲乙两地相距180千米,当车速度x(千米/小时)时,
f(x)=
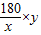 =
=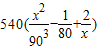 ,x∈(0,V]…6分(2)∵f(x)=
,x∈(0,V]…6分(2)∵f(x)=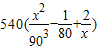 ,
,∴f′(x)=
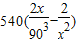
令f′(x)=0,解得x=90…8分
若V<90,有f′(x)<0,则函数f(x)在区间(0,V)内为单调减函数,所以车速为V(千米/小时)时,从甲地到乙地的耗油量最小;…11分
若V≥90,当0<x<90时,f′(x)<0;当90<x≤V时,f′(x)>0,所以,当x=90时,f(x)最小.…14分
综上:若V<90,车速为V(千米/小时)时,从甲地到乙地的耗油量最小;若V≥90,车速为90(千米/小时)时,从甲地到乙地的耗油量最小.…15
点评:本题考查的知识点是函数模型的选择与应用,利用导数求闭区间上的函数的最值,其中在建立函数模型时,由实际出发分析自变量的取值范围(定义域)是应用题的易忽略点,而(2)中要注意对V的取值进行分类讨论.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
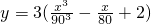 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时. (升)与速度
(升)与速度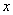 (千米/小时)的关系式为
(千米/小时)的关系式为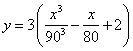 ,已知甲乙两地相距180千米,最高时速为
,已知甲乙两地相距180千米,最高时速为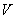 千米/小时。
千米/小时。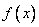 (升),求函数
(升),求函数