题目内容
某班设计了一个八边形的班徽（如图），它由腰长为
，顶角为
的四个等腰三角形及其底边构成的正方形所组成，则该八边形的面积为（ ）
A． | B． |
C． | D． |
A
解析试题分析：一个等腰三角形的面积为：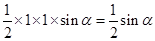
，由余弦定理得等腰三角形的底边长为：
，因此八边形的面积为：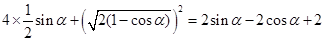
，故选择A.
考点：余弦定理及三角形面积公式.
练习册系列答案
相关题目
.
的最小正周期及
,且
,求
的值.△ABC中，已知
60°，如果△ABC 有两组解，则x的取值范围（ ）
A． | B． | C． | D． |
已知
中，三个内角A，B，C的对边分别为a,b,c，若的面积为S，且
等于
A． | B． | C． | D． |
在△ABC中，已知C＝
，
，△ABC的面积为
，则
=（ ）
A． | B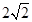． | C． | D． |
△ABC的内角
的对边分别为
，若成等比数列，且
，则
（ ）
A． | B． | C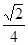． | D． |
在
中，满足下列条件的三角形有两个的是（ ）.
A． | B． |
C． | D． |
(2)
.在△ABC中，内角A，B，C所对的边分别是a，b，c.已知8b＝5c，C＝2B，则cos C＝( )
A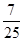． | B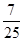．－ | C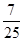．± | D． |