题目内容
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.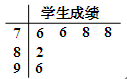
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设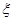 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求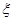 的分布列和期望.
的分布列和期望.
⑴这6位同学的成绩平均数为81;标准差为7;
⑵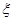 的分布列为
的分布列为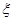
0 1 2 P 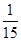
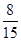
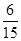
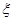 的数学期望为
的数学期望为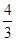 .
.
解析试题分析:⑴代入平均数及标准差的公式即得;⑵由(1)可得平均分为81,所以低于平均分的有4人,现从中抽取2人,随机变量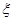 可能的取值为0,1,2.这是一个超几何分布,由超几何分布的概率公式即可得其分布列及期望.
可能的取值为0,1,2.这是一个超几何分布,由超几何分布的概率公式即可得其分布列及期望.
试题解析:⑴这6位同学的成绩平均数为 .
.
又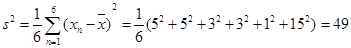 .
.
故这6位问学成绩的标准差为s=7 .6分
⑵随机变量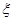 可能的取值为0,1,2,则
可能的取值为0,1,2,则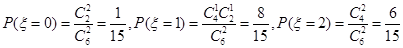 .
.
故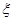 的分布列为
的分布列为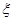
0 1 2 P 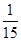
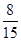
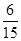
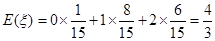
即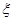 的数学期望
的数学期望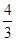 12分
12分
考点:1、平均数与标准差;2、随机变量的分布列及期望;3、超几何分布.

练习册系列答案
相关题目
阅读如图所示的程序框图,则输出结果 的值为( )
的值为( )
A. | B. | C. | D. |
程序框图如右图所示,则该程序运行后输出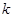 的值是( )
的值是( )
| A.5 | B.6 | C.7 | D.8 |
某程序框图如图所示,则该程序运行后输出的值是( )
| A.2 | B.-2 | C.3 | D.-3 |
某程序框图如右图所示,该程序运行后输出的k的值是( )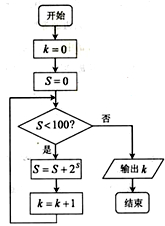
| A.4 | B.5 | C.6 | D.7 |
执行如图所示的程序框图,输出的S值为( )
| A.2 | B.4 | C.8 | D.16 |
根据给出的算法框图,计算 ( )
( )
A. | B. | C. | D. |
某算法的流程图如图所示,若输入a=4,b=2,c=6,则输出的结果为( )
| A.2 | B.4 | C.5 | D.6 |
执行如图所示的程序框图,若输出的结果为3,则可输入的实数x值的个数为()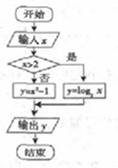
| A.1 |
| B.2 |
| C.4 |
| D.3 |