题目内容
设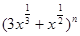 的二项展开式中各项系数之和为t,其二项式系数之和为h,若h+ t=272,则二项展开式为x2项的系数为
的二项展开式中各项系数之和为t,其二项式系数之和为h,若h+ t=272,则二项展开式为x2项的系数为
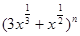 的二项展开式中各项系数之和为t,其二项式系数之和为h,若h+ t=272,则二项展开式为x2项的系数为
的二项展开式中各项系数之和为t,其二项式系数之和为h,若h+ t=272,则二项展开式为x2项的系数为 1
分析:给二项式中的x赋值1求出展开式的各项系数的和t;利用二项式系数和公式求出h,代入已知的等式,解方程求出n的值,得到表达式,求出二项式中x2项的系数即可.
解:令二项式中的x为1得到各项系数之和t=4n
又各项二项式系数之和h=2n
∵t+h=272,
∴4n+2n=272,
解得n=4,
所以
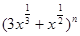 =(3x
=(3x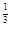 +x
+x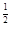 )4,
)4,它的展开式的通项为C
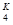 34-Kx
34-Kx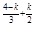 ,
,二项展开式中x2项时k=4,
二项展开式中x2项的系数为:1;
故答案为:1.

练习册系列答案
相关题目
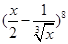 的展开式中常数项是( )
的展开式中常数项是( ) 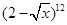 的展开式中不含
的展开式中不含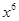 项的系数的和为
项的系数的和为 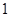 ,
,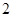 ,
,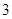 ,
,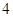 ,
,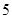 各一张,另一个盒子装有数字
各一张,另一个盒子装有数字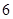 ,
,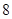 各一张,从两个盒子中各摸出一张卡片,则摸出两张数字为相邻整数卡片的概率是( )
各一张,从两个盒子中各摸出一张卡片,则摸出两张数字为相邻整数卡片的概率是( )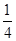
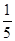
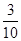
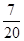
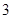 个不同的小球放入
个不同的小球放入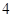 个盒子中,则不同放法种数有(....)
个盒子中,则不同放法种数有(....)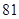 .....
.....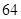 ...
...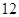 ...
...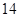
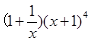 的展开式中
的展开式中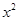 项的系数为 .
项的系数为 .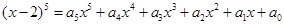 ,则
,则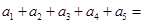 _______。
_______。