题目内容
(本小题满分12分)
如图所示,△ 是正三角形,
是正三角形,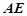 和
和 都垂直于平面
都垂直于平面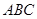 ,且
,且 ,
,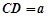 ,
,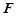 是
是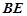 的中点.
的中点.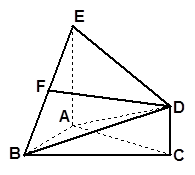
(1)求证: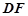 ∥平面
∥平面 ;
;
(2)求三棱锥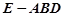 的体积.
的体积.
(1)只需证明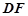 ∥
∥ ;(2)
;(2)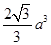 。
。
解析试题分析:(1)设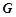 为
为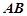 的中点,连
的中点,连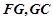 ,则
,则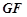 ∥
∥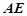 且
且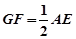 --------------2分
--------------2分
又  ∥
∥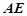 且
且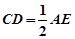
∴ ∥
∥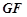 且
且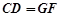 ,即四边形
,即四边形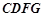 为平行四边形.------------4分
为平行四边形.------------4分
∴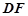 ∥
∥ 又
又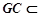 平面
平面
∴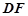 ∥平面
∥平面 ---------------------------------------6分
---------------------------------------6分
注:若学生用面面平行的性质解答,即证平面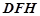 ∥平面
∥平面 ,按相应步骤给分.
,按相应步骤给分.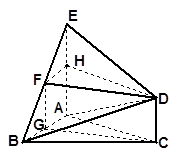
(2)∵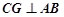
又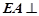 平面
平面 ,知
,知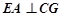
∴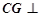 平面
平面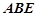 由(1)知
由(1)知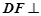 平面
平面
∴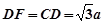 --------------------------------------------------8分
--------------------------------------------------8分
又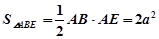
∴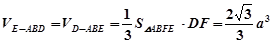 --------------------12分
--------------------12分
考点:线面垂直的性质定理;线面平行的判定定理;线面垂直的判定定理。
点评:立体几何中证明线面平行或面面平行都可转化为 线线平行,而证明线线平行一般有以下的一些方法: (1) 通过“平移”。 (2) 利用三角形中位线的性质。 (3) 利用平行四边形的性质。 (4) 利用对应线段成比例。 (5) 利用面面平行,等等。

练习册系列答案
相关题目
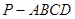 中,四边形
中,四边形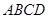 为正方形,
为正方形,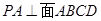 ,且
,且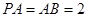 ,
,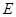 为
为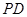 中点.
中点.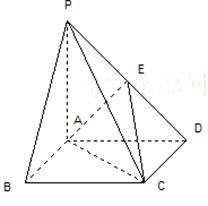
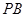 //平面
//平面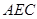 ;
;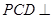 平面
平面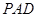 ;
;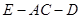 的正弦值.
的正弦值. 中,
中, ,
, ,
, .
. 
 平面
平面 ;
; ,且异面直线
,且异面直线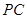 与
与 的夹角为
的夹角为 时,求二面角
时,求二面角 的余弦值.
的余弦值.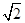 ,F是BC的中点.
,F是BC的中点.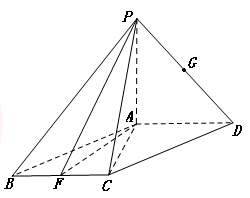
 ,
, ,
,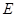 是
是 的中点,
的中点, 是
是 中点.
中点.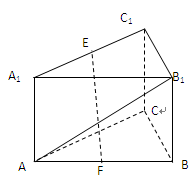
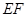 ∥面
∥面 ;
;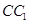 所成角的正切值;
所成角的正切值;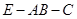 的平面角为
的平面角为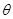 ,求
,求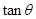 的值.
的值.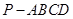 中,底面
中,底面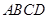 是正方形,侧面
是正方形,侧面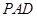 是正三角形,且平面
是正三角形,且平面
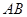 ⊥平面
⊥平面 与底面
与底面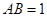 ,求点
,求点 到平面
到平面 的距离.
的距离. 中,
中,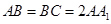
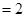 ,
, ,
, 是
是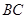 的中点.
的中点.
 平行平面
平行平面 ;
; 的余弦值;
的余弦值;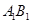 上是否存在点
上是否存在点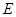 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定 中,四边形
中,四边形 为正方形,
为正方形, ,且
,且 ,
, 为
为 中点.
中点. //平面
//平面 ;
; 平面
平面 ;
; 的正弦值.
的正弦值.