题目内容
若f(x)=
,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )
| x |
分析:本题是用随机模拟的方法估算不规则图形的面积,若不规则图形的面积为S,模拟实验点的产生区域为Ω,则P≈
,结合实验所得频数与实验总次数,估算出频率,即得答案.
| S |
| Ω |
解答:解:在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,
由此得到30个点(xi,yi)(i=1,2,…,30),
即所有基本事件Ω共有30个
而其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,
即满足条件基本事件共有10个
则y=f(x)与x=4及x轴围成的面积S满足
≈
即S≈
故选B
由此得到30个点(xi,yi)(i=1,2,…,30),
即所有基本事件Ω共有30个
而其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,
即满足条件基本事件共有10个
则y=f(x)与x=4及x轴围成的面积S满足
| S |
| 4×4 |
| 10 |
| 30 |
即S≈
| 16 |
| 3 |
故选B
点评:本题考查的知识点是随机模拟实验,其中当不规则图形的面积为S,模拟实验点的产生区域为Ω时,则P≈
是解任本题的关键.
| S |
| Ω |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:f(x)=20|x-4|(x≥1),g(x)=
(x-4)2(x≥1),h(x)=
|log2x-
-
|(x≥1),其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | 0 | … |
| 20 |
| 3 |
| 240 |
| 11 |
| 1 |
| x |
| 7 |
| 4 |
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
一化工厂因排污趋向严重,2011年1月决定着手整治.经调研,该厂第一个月的污染度为60,整治后前四个月的污染度如下表;
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | 0 | … |
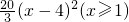 ,h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.(参考数据:lg2=0.3010,lg3=0.4771)
,h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.(参考数据:lg2=0.3010,lg3=0.4771)(Ⅰ)问选用哪个函数模拟比较合理,并说明理由;
(Ⅱ)如果环保部门要求该厂每月的排污度均不能超过60,若以比较合理的模拟函数预测,该厂最晚在何时开始进行再次整治?