题目内容
如右图,在圆的内接四边形ABCD中, ,
, 则BC=______.
则BC=______.

解析试题分析:由题得,因为四边形ABCD是圆的内接四边形,所以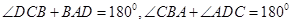 ,又因为
,又因为 ,
, 所以
所以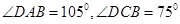 ,则由
,则由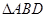 与
与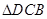 的正弦定理得
的正弦定理得 与
与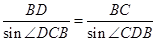 ,即
,即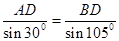 =
=
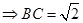 ,故填
,故填
考点:正弦定理

练习册系列答案
相关题目
题目内容
如右图,在圆的内接四边形ABCD中, ,
, 则BC=______.
则BC=______.

解析试题分析:由题得,因为四边形ABCD是圆的内接四边形,所以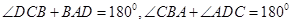 ,又因为
,又因为 ,
, 所以
所以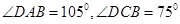 ,则由
,则由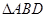 与
与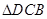 的正弦定理得
的正弦定理得 与
与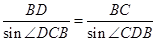 ,即
,即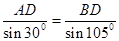 =
=
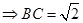 ,故填
,故填
考点:正弦定理
