题目内容
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
(Ⅰ)证明EF//平面A1CD;
(Ⅱ)证明平面A1CD⊥平面A1ABB1;
(Ⅲ)求直线BC与平面A1CD所成角的正弦值.
(Ⅰ)详见解题分析;(Ⅱ)详见解题分析;(Ⅲ)直线 与平面
与平面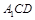 所成角的正弦值为
所成角的正弦值为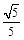 .
.
解析试题分析:(Ⅰ)如图,在三棱柱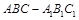 中,要证明
中,要证明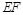 //平面
//平面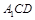 ,只要在平面
,只要在平面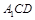 内找
内找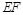 的平行线,也即只要证明
的平行线,也即只要证明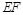 //
//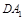 即可.需要先证明四边形
即可.需要先证明四边形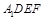 为平行四边形,这可有
为平行四边形,这可有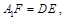 且
且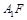 //
//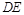 得到;(Ⅱ)要证明平面
得到;(Ⅱ)要证明平面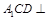 平面
平面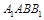 ,只要能在其中一个平面内找到另一个平面的垂线即可.可以尝试证明
,只要能在其中一个平面内找到另一个平面的垂线即可.可以尝试证明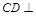 平面
平面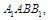 由于
由于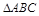 是正三角形,
是正三角形,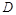 为
为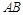 的中点,故
的中点,故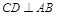 ,为此只要证明
,为此只要证明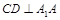 ,它可以利益
,它可以利益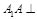 底面
底面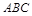 得到;(Ⅲ)首先需找到或作出线
得到;(Ⅲ)首先需找到或作出线 与平面
与平面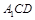 所成角.按照定义,结合已知,在平面
所成角.按照定义,结合已知,在平面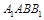 内,过点
内,过点 作
作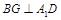 交直线
交直线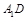 于点
于点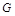 ,连接
,连接 .再利用面面垂直的性质定理,证明
.再利用面面垂直的性质定理,证明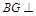 平面
平面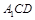 .由此得
.由此得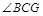 为直线
为直线 与平面
与平面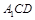 所成角.最后在
所成角.最后在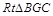 中,利用锐角三角函数求直线
中,利用锐角三角函数求直线 与平面
与平面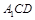 所成角的正弦值.
所成角的正弦值.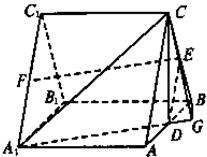
试题解析:(Ⅰ)证明:如图,在三棱柱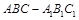 中,
中, //
//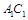 ,且
,且 连接
连接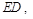 在
在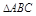 中,
中,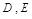 分别为
分别为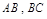 的中点,
的中点,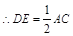 且
且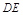 //
//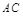 ,又
,又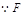 为
为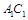 的中点,可得
的中点,可得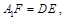 且
且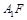 //
//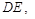 即四边形
即四边形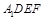 为平行四边形,
为平行四边形,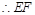 //
//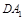 .又
.又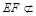 平面
平面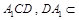 平面
平面
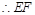 //平面
//平面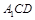 ;
;
(Ⅱ)证明:由于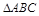 是正三角形,
是正三角形,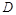 为
为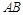 的中点,故
的中点,故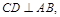 又由于侧棱
又由于侧棱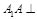 底面
底面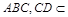 底面
底面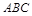 ,
,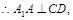
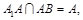 因此
因此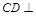 平面
平面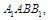
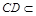 平面
平面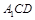 ,
,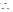 平面
平面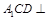 平面
平面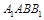 ;
;
(Ⅲ)解:在平面
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 中,
中,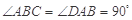 ,
, ,
,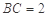 ,
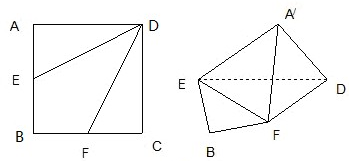
,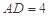 . 把
. 把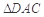 沿对角线
沿对角线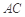 折起到
折起到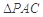 的位置,如图2所示,使得点
的位置,如图2所示,使得点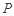 在平面
在平面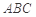 上的正投影
上的正投影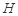 恰好落在线段
恰好落在线段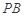 ,点
,点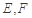 分别为线段
分别为线段 的中点.
的中点. 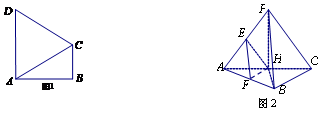
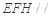 平面
平面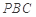 ;
;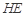 与平面
与平面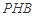 所成角的正弦值;
所成角的正弦值;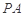 上是否存在一点
上是否存在一点 ,使得
,使得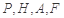 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.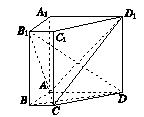
 中,
中,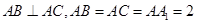 ,点
,点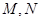 分别为
分别为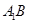 和
和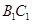 的中点.
的中点.
 平面
平面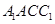 ;
;
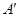
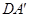 ⊥EF;
⊥EF;
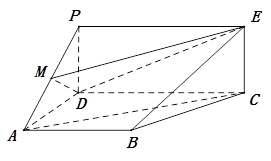
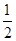 CD=1,PD=
CD=1,PD= 。
。
 ?
?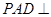 平面
平面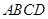 ,
,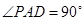 ,且
,且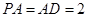 ,
, 、
、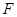 、
、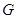 分别是线段
分别是线段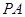 、
、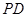 、
、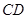 的中点.
的中点.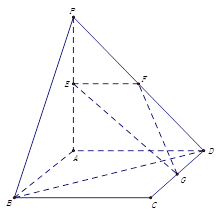
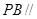 平面
平面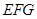 ;
;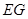 、
、 所成角的余弦值.
所成角的余弦值.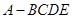 中,侧面
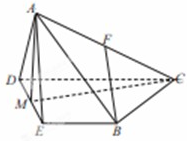
中,侧面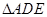 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形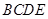 中,
中, ,
, ,
, ,
, ,
,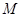 为
为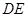 的中点,
的中点, 为
为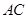 的中点,
的中点,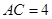 .
.
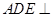 平面
平面 ;
;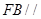 平面
平面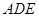 .
.