题目内容
已知向量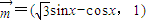 ,
,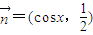 ,若
,若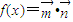 .
.(Ⅰ) 求函数f(x)的最小正周期;
(Ⅱ) 已知△ABC的三内角A、B、C的对边分别为a、b、c,且a=3,
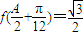 (A为锐角),2sinC=sinB,求A、c、b的值.
(A为锐角),2sinC=sinB,求A、c、b的值.
【答案】分析:(Ⅰ)利用两角和差的正弦公式化简函数f(x)的解析式为sin(2x-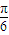 ),由此求得函数f(x)的最小正周期.
),由此求得函数f(x)的最小正周期.
(Ⅱ) 已知△ABC中,由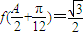 (A为锐角),求得sinA=
(A为锐角),求得sinA= ,可得 A=
,可得 A=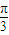 .由正弦定理可得b=2c,根据 a=3,再由余弦定理求出c、b的值.
.由正弦定理可得b=2c,根据 a=3,再由余弦定理求出c、b的值.
解答:解:(Ⅰ)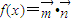 =
=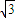 sinxcosx-cos2x+
sinxcosx-cos2x+ =
=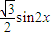 -
-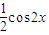 =sin(2x-
=sin(2x- ),故函数f(x)的最小正周期为π.
),故函数f(x)的最小正周期为π.
(Ⅱ) 已知△ABC中,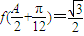 (A为锐角),∴sinA=
(A为锐角),∴sinA=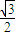 ,∴A=
,∴A=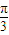 .
.
∵2sinC=sinB,∴由正弦定理可得b=2c,
∵a=3,再由余弦定理可得 9=b2+c2-2bc•cos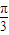 .
.
解得 b=2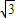 ,c=
,c=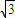 .
.
点评:本题主要考查两个向量的数量积公式,两角和差的正弦公式、正弦定理、余弦定理的应用,属于中档题.
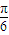 ),由此求得函数f(x)的最小正周期.
),由此求得函数f(x)的最小正周期.(Ⅱ) 已知△ABC中,由
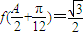 (A为锐角),求得sinA=
(A为锐角),求得sinA= ,可得 A=
,可得 A=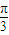 .由正弦定理可得b=2c,根据 a=3,再由余弦定理求出c、b的值.
.由正弦定理可得b=2c,根据 a=3,再由余弦定理求出c、b的值.解答:解:(Ⅰ)
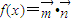 =
=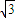 sinxcosx-cos2x+
sinxcosx-cos2x+ =
=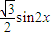 -
-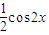 =sin(2x-
=sin(2x- ),故函数f(x)的最小正周期为π.
),故函数f(x)的最小正周期为π.(Ⅱ) 已知△ABC中,
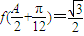 (A为锐角),∴sinA=
(A为锐角),∴sinA=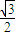 ,∴A=
,∴A=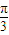 .
.∵2sinC=sinB,∴由正弦定理可得b=2c,
∵a=3,再由余弦定理可得 9=b2+c2-2bc•cos
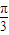 .
.解得 b=2
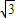 ,c=
,c=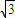 .
.点评:本题主要考查两个向量的数量积公式,两角和差的正弦公式、正弦定理、余弦定理的应用,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 ,
, ,若
,若 与
与 垂直,则
垂直,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.
 ,
,
 ,
, ,求
,求 和
和 的值;
的值; ,求
,求 的值.
的值. =
=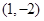 ,
, =
= ,若
,若 B.
B. C.
C.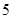 D.
D.
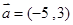 ,
, ,若向量
,若向量 、
、 互相平行,则
互相平行,则 =____________.
=____________.