题目内容
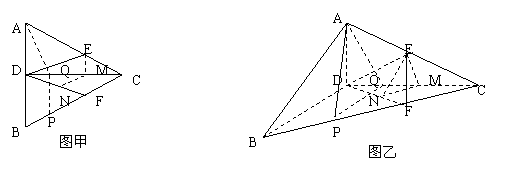
(12分)如图甲,正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,先将△ABC沿CD折叠成直二面角A-DC-B(如图乙),在乙图中
(Ⅰ)求二面角E-DF-C的余弦值;
(Ⅱ)在线段BC上找一点P,使AP⊥DE,并求BP.
(Ⅲ)求三棱锥D-ABC外接球的表面积.(只需用数字回答,可不写过程)
 |
【答案】
解:(1)∵AD⊥CD,BD⊥CD,∴∠ADB是二面角A-CD-B的平角
∴ AD⊥BD ∴AD⊥平面BCD,取CD的中点M,这时EM∥AD,∴EM⊥平面BCD
过M作MN⊥DF于点N,连结EN,则EN⊥DF
∴∠MNE是二面角E-DF-N的平面角…………………………2分
在 Rt△EMN中,EM=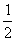 AD=
AD=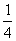 AB=1,
AB=1,
 MN=
MN=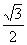 ∴EN=
∴EN=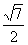 ,cos∠MNE=
,cos∠MNE=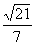 ………4分
………4分
(2)在线段BC上取点P,使BP=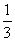 BC=
BC=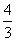 ,
,
过P作PQ⊥CD于点Q, ∴ PQ⊥平面ACD
∵DQ=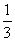 DC=
DC=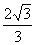 ,在等边△ADE中,∠DAQ=30
,在等边△ADE中,∠DAQ=30
∴AQ⊥DE,∴AP⊥DE……………………8分
(3)2R=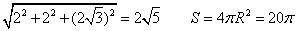 ………………12分
………………12分

练习册系列答案
相关题目
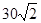 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于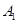 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西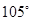 方向的
方向的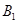 处,此时两船相距
处,此时两船相距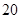 海里,当甲船航行
海里,当甲船航行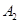 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西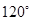 方向的
方向的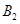 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?(结论保留根号形式)
海里,问乙船每小时航行多少海里?(结论保留根号形式)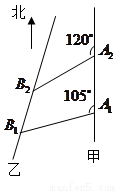
 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时。
海里/小时。
 。
。 时,求两船出发后多长时间距离最近,最近距离为多少海里?
时,求两船出发后多长时间距离最近,最近距离为多少海里?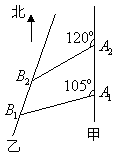 如图,甲船以每小时
如图,甲船以每小时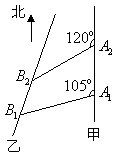 如图,甲船以每小时
如图,甲船以每小时 (1)求处于
(1)求处于