题目内容
设 、
、 、
、 是单位向量,且
是单位向量,且 =0,则
=0,则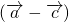 •
•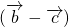 的最小值为
的最小值为
- A.-2
- B.
 -2
-2 - C.-1
- D.1-

D
分析:由题意可得 =
= ,故要求的式子即
,故要求的式子即  -(
-( )•
)• +
+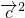 =1-
=1- cos
cos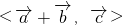 =1-
=1- cos
cos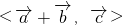 ,再由余弦函数的值域求出它的最小值.
,再由余弦函数的值域求出它的最小值.
解答:∵ 、
、 、
、 是单位向量,
是单位向量, ,∴
,∴ ,
, =
= .
.
∴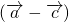 •
•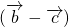 =
= -(
-( )•
)• +
+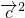 =0-(
=0-( )•
)• +1=1-
+1=1- cos
cos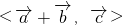
=1- cos
cos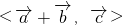 ≥
≥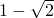 .
.
故选项为D
点评:考查向量的运算法则;交换律、分配律但注意不满足结合律.
分析:由题意可得
 =
= ,故要求的式子即
,故要求的式子即  -(
-( )•
)• +
+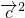 =1-
=1- cos
cos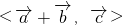 =1-
=1- cos
cos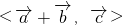 ,再由余弦函数的值域求出它的最小值.
,再由余弦函数的值域求出它的最小值.解答:∵
 、
、 、
、 是单位向量,
是单位向量, ,∴
,∴ ,
, =
= .
.∴
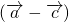 •
•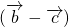 =
= -(
-( )•
)• +
+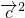 =0-(
=0-( )•
)• +1=1-
+1=1- cos
cos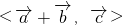
=1-
 cos
cos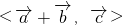 ≥
≥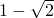 .
.故选项为D
点评:考查向量的运算法则;交换律、分配律但注意不满足结合律.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 ,
, ,
,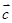 是单位向量,且
是单位向量,且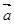 、
、 、
、 是单位向量,且
是单位向量,且 ,则
,则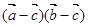 的最小值为
的最小值为 -2
-2 、
、 、
、 是单位向量,且
是单位向量,且 ,则
,则 的最小值为
(
)
的最小值为
(
)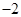 B.
B. C.
C. D.
D.