题目内容
统计某产品的广告费用x与销售额y的一组数据如下表:
|
分析:先求样本中心点,再代入回归直线方程,即可求得m的值.
解答:解:由题意,
=
=4,
=
=7+
∵y对x的回归直线方程是
,
∴7+
=4.4+4.6,∴m=8
故选B.
. |
| x |
| 2+3+5+6 |
| 4 |
. |
| y |
| 7+m+9+12 |
| 4 |
| m |
| 4 |
∵y对x的回归直线方程是
| ||
∴7+
| m |
| 4 |
故选B.
点评:本题考查回归直线方程,解题的关键是利用回归直线方程恒过样本中心点,属于基础题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知统计某产品的广告费用 (万元)与销售额
(万元)与销售额 (万元)所得的数据如下表所示:
(万元)所得的数据如下表所示:
|
|
0 |
1 |
3 |
4 |
|
|
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析, 与
与 有较强的线性相关性,且
有较强的线性相关性,且 ,则
,则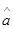 等于
等于
A. 2.6万元 B. 2.4万元 C. 2.7万元 D. 2.5万元
统计某产品的广告费用x与销售额y的一组数据如下表:
|
广告费用 |
2 |
3 |
5 |
6 |
|
销售额 |
7 |
|
9 |
12 |
若根据上表提供的数据用最小二乘法可求得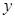 对
对 的回归直线方程是
的回归直线方程是 ,则数据中的
,则数据中的 的值应该是( )
的值应该是( )
A.7.9 B.8 C.8.1 D.9
统计某产品的广告费用x与销售额y的一组数据如下表:
若根据上表提供的数据用最小二乘法可求得y对x的回归直线方程是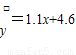 ,则数据中的m的值应该是( )
,则数据中的m的值应该是( )
A.7.9
B.8
C.8.1
D.9
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
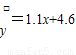 ,则数据中的m的值应该是( )
,则数据中的m的值应该是( )A.7.9
B.8
C.8.1
D.9