题目内容
若函数y=
(m>0)在x0处的导数等于0,那么x0等于( )
| x2+m2 |
| x |
分析:利用求导数的公式和导数的运算法则,得导函数,又由f′(x0)=0,所得到的解即为本题答案.
解答:解:由于函数y=
=x+
(m>0),则y′=1-
(m>0)
又由函数在x0处的导数等于0,即f′(x0)=0,亦即1-
=0(m>0),解得x0=±m.
故答案为 C.
| x2+m2 |
| x |
| m2 |
| x |
| m2 |
| x2 |
又由函数在x0处的导数等于0,即f′(x0)=0,亦即1-
| m2 |
| x02 |
故答案为 C.
点评:本题着重考查了求导数的公式和导数的运算法则等知识,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
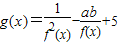 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.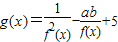 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.