题目内容
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为| 1 | 3 |
(Ⅰ)求此公司决定对该项目投资的概率;
(Ⅱ)记投票结果中“中立”票的张数为随机变量ξ,求ξ的分布列及数学期望Eξ.
分析:(1)此公司决定对该项目投资包括两种情况,一是投票结果中有两张“同意”票,二是投票结果中三张“同意”票,投票相互没有影响,根据符号独立重复试验,得到此公司决定对该项目投资的概率.
(2)由题意知投票结果中“中立”票的张数对应的随机变量ξ的可能取值是0、1、2、3,利用独立重复试验的概率公式求出变量的概率,写出分布列和期望.
(2)由题意知投票结果中“中立”票的张数对应的随机变量ξ的可能取值是0、1、2、3,利用独立重复试验的概率公式求出变量的概率,写出分布列和期望.
解答:解:(1)此公司决定对该项目投资包括两种情况,
一是投票结果中有两张“同意”票,二是投票结果中三张“同意”票,
投票相互没有影响
∴此公司决定对该项目投资的概率为
P=C32(
)2(
)+C33(
)3=
(2)ξ的取值为0、1、2、3
P(ξ=0)=(1-
)3=
P(ξ=1)=C31(
)(
)2=
P(ξ=2)=C32(
)2(
)=
P(ξ=3)=(
)3=
∴ξ的分布列为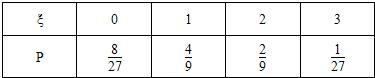
∴Eξ=nP=3×
=1
一是投票结果中有两张“同意”票,二是投票结果中三张“同意”票,
投票相互没有影响
∴此公司决定对该项目投资的概率为
P=C32(
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 7 |
| 27 |
(2)ξ的取值为0、1、2、3
P(ξ=0)=(1-
| 1 |
| 3 |
| 8 |
| 27 |
P(ξ=1)=C31(
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(ξ=2)=C32(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
P(ξ=3)=(
| 1 |
| 3 |
| 1 |
| 27 |
∴ξ的分布列为

∴Eξ=nP=3×
| 1 |
| 3 |
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是重点,这种题目高考必考,应注意解题的格式.

练习册系列答案
相关题目