题目内容
如果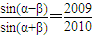 ,则
,则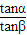 =( )
=( )A.
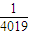
B.
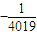
C.4019
D.-4019
【答案】分析:将分式转化为整式,利用和、差角的正弦公式展开进行合并整理是解决本题的关键,注意正弦、余弦、正切之间的转化问题,注意切化弦的方法和整体思想的运用.
解答:解:由题意可得2010sinαcosβ-2010cosαsinβ=2009sinαcosβ+2009cosαsinβ,
∴sinαcosβ=4019cosαsinβ,得tanα=4019tanβ,∴ .
.
故选C.
点评:本题考查三角恒等变换的基本知识,考查了两角和与差的正弦公式,主要寻找角之间的关系和函数名称之间的关系,考查同角三角函数的基本关系式,注意整体思想的运用.考查转化与化归思想的应用.
解答:解:由题意可得2010sinαcosβ-2010cosαsinβ=2009sinαcosβ+2009cosαsinβ,
∴sinαcosβ=4019cosαsinβ,得tanα=4019tanβ,∴
 .
.故选C.
点评:本题考查三角恒等变换的基本知识,考查了两角和与差的正弦公式,主要寻找角之间的关系和函数名称之间的关系,考查同角三角函数的基本关系式,注意整体思想的运用.考查转化与化归思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
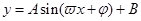 的一部分图象如右图所示,
的一部分图象如右图所示,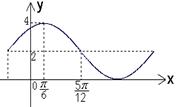
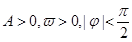 ,则( )
,则( ) 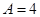 B.
B. C.
C.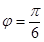 D.
D.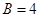
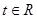 设
设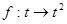 是集合P到集合Q的映射,如果Q
是集合P到集合Q的映射,如果Q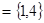 则
则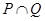 =( )。
=( )。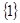 B、
B、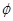 C、
C、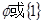 D、
D、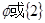
 中,如果有
中,如果有 ,则此三角形是
,则此三角形是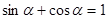 ,则
,则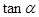 =( )
=( )