题目内容
已知
=（3，4），
=（-6，-8），则向量
与
（ ）
| a |
| b |
| a |
| b |
分析：由题意可得|
|、|
|以及
•
的值．再利用两个向量的夹角公式求得向量
与
的夹角，从而得出结论
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：由题意可得|
|=5，|
|=10，
•
=-18-32=-50．
设向量
与
的夹角为θ，则由cosθ=
=-1，可得θ=180°，
故向量
与
互相平行，
故选A．
| a |
| b |
| a |
| b |
设向量
| a |
| b |
| ||||
|
|
故向量
| a |
| b |
故选A．
点评：本题主要考查用数量积表示两个两个向量的夹角，两个向量共线的定义，属于中档题．
练习册系列答案
相关题目
已知a=（3，4），b⊥a，且b的起点为（1，2），终点为（x，3x），则b等于（ ）
A、（-
| ||||
B、（-
| ||||
C、（-
| ||||
D、（
|
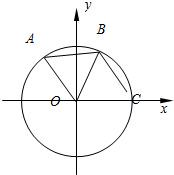如图：A，B是圆O上的两点，点C是圆O与x轴正半轴的交点，已知A（-3，4），且点B在劣弧CA上，△AOB为正三角形．