题目内容
已知向量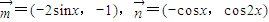 ,定义f(x)=
,定义f(x)=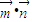
(1)求函数f(x)的表达式,并求其单调增区间;
(2)在锐角△ABC中,角A、B、C对边分别为a、b、c,且f(A)=1,bc=8,求△ABC的面积.
【答案】分析:(1)通过向量的数量积,二倍角的三角函数求函数f(x)的表达式,通过正弦函数的单调增区间求其单调增区间;
(2)利用f(A)=1,求出A的值,利用bc=8,通过△ABC的面积公式求解即可.
解答:解:(1)因为已知向量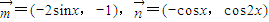 ,
,
f(x)=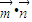 =2sin2x-cos2x=
=2sin2x-cos2x=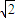 sin(2x-
sin(2x-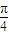 )…(3分)
)…(3分)
令2kπ-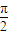 ≤2x-
≤2x-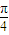 ≤2kπ+
≤2kπ+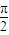 ,k∈Z,
,k∈Z,
解得kπ-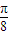 ≤x≤kπ+
≤x≤kπ+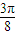 .
.
所以,函数f(x)的单调递增区间为[kπ-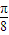 ,kπ+
,kπ+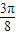 ],k∈Z.…(6分)
],k∈Z.…(6分)
(2)∵f(A)=1,
∴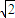 sin(2A-
sin(2A-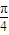 )=1,
)=1,
∴2A-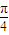 =2Kπ+
=2Kπ+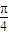
∴A=kπ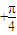 ,又△ABC为锐角三角形,
,又△ABC为锐角三角形,
则A=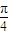 ,又bc=8,
,又bc=8,
则△ABC的面积S= bcsinA=
bcsinA= ×8×
×8×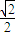 =2
=2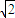 .…(12分)
.…(12分)
点评:题考查了平面向量的数量积运算,二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,三角形的面积公式,以及特殊角的三角函数值,熟练掌握公式及法则是解本题的关键.
(2)利用f(A)=1,求出A的值,利用bc=8,通过△ABC的面积公式求解即可.
解答:解:(1)因为已知向量
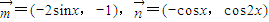 ,
,f(x)=
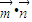 =2sin2x-cos2x=
=2sin2x-cos2x=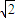 sin(2x-
sin(2x-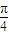 )…(3分)
)…(3分)令2kπ-
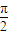 ≤2x-
≤2x-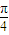 ≤2kπ+
≤2kπ+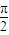 ,k∈Z,
,k∈Z,解得kπ-
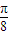 ≤x≤kπ+
≤x≤kπ+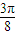 .
.所以,函数f(x)的单调递增区间为[kπ-
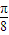 ,kπ+
,kπ+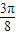 ],k∈Z.…(6分)
],k∈Z.…(6分)(2)∵f(A)=1,
∴
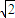 sin(2A-
sin(2A-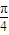 )=1,
)=1,∴2A-
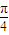 =2Kπ+
=2Kπ+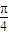
∴A=kπ
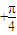 ,又△ABC为锐角三角形,
,又△ABC为锐角三角形,则A=
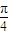 ,又bc=8,
,又bc=8,则△ABC的面积S=
 bcsinA=
bcsinA= ×8×
×8×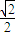 =2
=2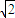 .…(12分)
.…(12分)点评:题考查了平面向量的数量积运算,二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,三角形的面积公式,以及特殊角的三角函数值,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
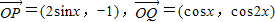 ,定义函数
,定义函数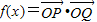 .
. ,定义函数
,定义函数 .
.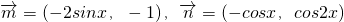 ,定义f(x)=
,定义f(x)=