题目内容
随着现代社会的发展，拥有汽车的家庭越来越多，交通安全显得尤为重要，考取汽车驾驶执照要求也越来越高．某汽车驾驶学校在学员结业前对其驾驶技术进行4次考核，规定：按顺序考核，一旦考核合格，不必参加以后的考核，否则还需参加下次考核．若小明参加每次考核合格的概率依次组成一个公差为| 1 |
| 7 |
| 1 |
| 2 |
| 15 |
| 49 |
分析：（1）设出小明参加第一次考核就合格的概率，根据他直到参加第二次考核才合格的概率为
，和小明参加每次考核合格的概率依次组成一个公差为
的等差数列，写出关系式，得到方程，解方程即可，注意去掉不合题意的．
（2）由（1）知，小明参加每次考核合格的概率依次是
，
，
，1，变量的可能取值是1，2，3，4，根据相互独立事件的概率公式得到变量对应的概率，写出分布列和期望值．
| 15 |
| 49 |
| 1 |
| 7 |
（2）由（1）知，小明参加每次考核合格的概率依次是
| 4 |
| 7 |
| 5 |
| 7 |
| 6 |
| 7 |
解答：解：（1）设小明参加第一次考核就合格的概率为p，
则(1-p)(P+
•)=
即49p2-42p+8=O，
解得：P=
或P=
∵p=.
＜
，
∴p=
即小明参加第一次考核就合格的概率为
（2）由（1）知，小明参加每次考核合格的概率依次是
，
，
，1
∴ξ=1，2，3，4，
P（ξ=1）=
，P（ξ=2）=
P(ξ=3)=(1-
)×(1-
)×
=
P(ξ=4)=(1-
)×(1-
)×(1-
)×1=
∴ξ的分布列为
∴Eξ=1×
+2×
+3×
+4×
=
则(1-p)(P+
| 1 |
| 7 |
| 15 |
| 49 |
即49p2-42p+8=O，
解得：P=
| 2 |
| 7 |
| 4 |
| 7 |
∵p=.
| 2 |
| 7 |
| 1 |
| 2 |
∴p=
| 4 |
| 7 |
即小明参加第一次考核就合格的概率为
| 4 |
| 7 |
（2）由（1）知，小明参加每次考核合格的概率依次是
| 4 |
| 7 |
| 5 |
| 7 |
| 6 |
| 7 |
∴ξ=1，2，3，4，
P（ξ=1）=
| 4 |
| 7 |
| 15 |
| 49 |
P(ξ=3)=(1-
| 4 |
| 7 |
| 5 |
| 7 |
| 6 |
| 7 |
| 36 |
| 343 |
P(ξ=4)=(1-
| 4 |
| 7 |
| 5 |
| 7 |
| 6 |
| 7 |
| 6 |
| 343 |
∴ξ的分布列为
∴Eξ=1×
| 4 |
| 7 |
| 15 |
| 49 |
| 36 |
| 343 |
| 6 |
| 343 |
| 538 |
| 343 |
点评：本题考查离散型随机变量的分布列和期望值，考查相互独立事件的概率公式，考查对立事件的概率，本题是一个综合题目，是近几年必出的一道题目．
练习册系列答案
相关题目
的等差数列，且他参加第一次考核合格的概率大于
，他直到参加第二次考核才合格的概率为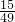
．（1）求小明参加第一次考核就合格的概率；（2）求小明参加考核的次数ξ的分布列和数学期望．
的等差数列，且他参加第一次考核合格的概率大于
，他直到参加第二次考核才合格的概率为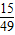
．（1）求小明参加第一次考核就合格的概率；（2）求小明参加考核的次数ξ的分布列和数学期望．