题目内容
已知曲线C:y=x2与直线l:x-y+2=0交于两点A(xA,yA)和B(xB,yB),且xA<xB.记曲线C在点A和点B之间那一段L与线段AB所围成的平面区域(含边界)为D.设点P(s,t)是L上的任一点,且点P与点A和点B均不重合.(1)若点Q是线段AB的中点,试求线段PQ的中点M的轨迹方程;
(2)若曲线G:x2-2ax+y2-4y+a2+
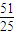 =0与D有公共点,试求a的最小值.
=0与D有公共点,试求a的最小值.
【答案】分析:(1)欲求线段PQ的中点M的轨迹方程,设线段PQ的中点M坐标为(x,y),即要求x,y间的关系式,先利用x,y列出点P(s,t)的坐标结合点P在曲线C上即得;
(2)处理圆与D有无公共点的问题,须分两种情形讨论:当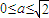 时和当a<0时.对于后一种情形,只须只需考虑圆心E到直线l:x-y+2=0的距离即可,从而求得求a的最小值.
时和当a<0时.对于后一种情形,只须只需考虑圆心E到直线l:x-y+2=0的距离即可,从而求得求a的最小值.
解答: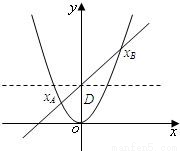 解:(1)联立y=x2与y=x+2得xA=-1,xB=2,则AB中点
解:(1)联立y=x2与y=x+2得xA=-1,xB=2,则AB中点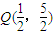 ,设线段PQ的中点M坐标为(x,y),则
,设线段PQ的中点M坐标为(x,y),则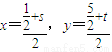 ,即
,即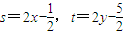 ,又点P在曲线C上,
,又点P在曲线C上,
∴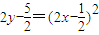 化简可得
化简可得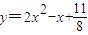 ,
,
又点P是L上的任一点,且不与点A和点B重合,
则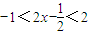 ,即
,即 ,
,
∴中点M的轨迹方程为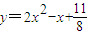 (
(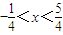 ).
).
(2)曲线G:x2-2ax+y2-4y+a2+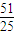 =0,
=0,
即圆E: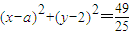 ,其圆心坐标为E(a,2),半径
,其圆心坐标为E(a,2),半径
由图可知,当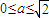 时,曲线G:x2-2ax+y2-4y+a2+
时,曲线G:x2-2ax+y2-4y+a2+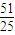 =0与点D有公共点;
=0与点D有公共点;
当a<0时,要使曲线G:x2-2ax+y2-4y+a2+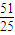 =0与点D有公共点,
=0与点D有公共点,
只需圆心E到直线l:x-y+2=0的距离
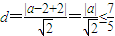 ,
,
得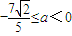 ,则a的最小值为
,则a的最小值为 .
.
点评:本小题主要考查直线与圆锥曲线的综合问题、轨迹方程、抛物线方程、圆的方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.
(2)处理圆与D有无公共点的问题,须分两种情形讨论:当
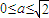 时和当a<0时.对于后一种情形,只须只需考虑圆心E到直线l:x-y+2=0的距离即可,从而求得求a的最小值.
时和当a<0时.对于后一种情形,只须只需考虑圆心E到直线l:x-y+2=0的距离即可,从而求得求a的最小值.解答:
 解:(1)联立y=x2与y=x+2得xA=-1,xB=2,则AB中点
解:(1)联立y=x2与y=x+2得xA=-1,xB=2,则AB中点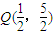 ,设线段PQ的中点M坐标为(x,y),则
,设线段PQ的中点M坐标为(x,y),则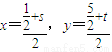 ,即
,即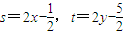 ,又点P在曲线C上,
,又点P在曲线C上,∴
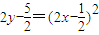 化简可得
化简可得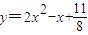 ,
,又点P是L上的任一点,且不与点A和点B重合,
则
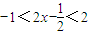 ,即
,即 ,
,∴中点M的轨迹方程为
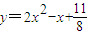 (
(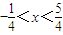 ).
).(2)曲线G:x2-2ax+y2-4y+a2+
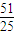 =0,
=0,即圆E:
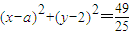 ,其圆心坐标为E(a,2),半径
,其圆心坐标为E(a,2),半径
由图可知,当
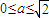 时,曲线G:x2-2ax+y2-4y+a2+
时,曲线G:x2-2ax+y2-4y+a2+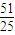 =0与点D有公共点;
=0与点D有公共点;当a<0时,要使曲线G:x2-2ax+y2-4y+a2+
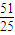 =0与点D有公共点,
=0与点D有公共点,只需圆心E到直线l:x-y+2=0的距离
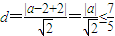 ,
,得
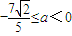 ,则a的最小值为
,则a的最小值为 .
.点评:本小题主要考查直线与圆锥曲线的综合问题、轨迹方程、抛物线方程、圆的方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.