题目内容
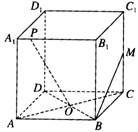
(07年崇文区一模理) 如图,在正方体ABCD―A1B1C1D1中,M是C1C的中点,O是底面ABCD的中心,P是A1B1上的任意点,则直线BM与OP所成的角为 .
答案:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(07年崇文区一模理) 如图,在正方体ABCD―A1B1C1D1中,M是C1C的中点,O是底面ABCD的中心,P是A1B1上的任意点,则直线BM与OP所成的角为 .

答案:![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案