题目内容
在四棱锥 ,
, 平面
平面 ,
, ,
, ,
, ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)当点 到平面
到平面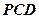 的距离为
的距离为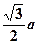 时,求二面角
时,求二面角 的余弦值;
的余弦值;
(3)当 为何值时,点
为何值时,点 在平面
在平面 内的射影
内的射影 恰好是
恰好是 的重心.
的重心.
(1)连接 交
交 于
于 ,易知
,易知 ,而
,而 面
面 ,
, ,又
,又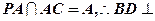 面
面 ,又
,又 面
面 ,
, 平面
平面 平面
平面 (4分)
(4分)
(2)由 面
面 得
得 ,又
,又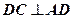 ,
,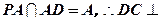 面
面
又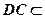 面
面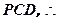 面
面
 面
面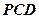 (5分)
(5分)
过 作
作 于
于 面
面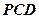 ,
, 是点
是点 到平面
到平面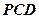 的距离(6分)故
的距离(6分)故
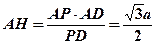 (8分)所以
(8分)所以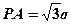
作 于
于 ,连接
,连接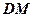 ,
,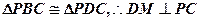 ,
, 为所求
为所求
在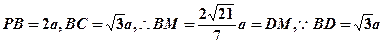 ,
,
(3)连接 ,则重心
,则重心 在
在 上,且
上,且 ,连接
,连接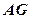 (9分)
(9分)
已知 面
面 ,所以
,所以 (10分),
(10分),
由 可得
可得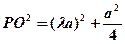 ,解得
,解得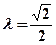
解析

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
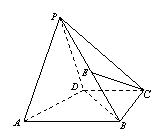
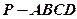 ,
, 平面
平面 ,
, ,
, ,
, ,
, .
.
 平面
平面 ;
; 到平面
到平面 的距离为
的距离为 时,求二面角
时,求二面角 的余弦值;
的余弦值; 为何值时,点
为何值时,点 内的射影
内的射影 恰好是
恰好是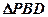 的重心.
的重心.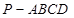 中,
中, 平面
平面 ,
,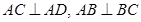 ,
,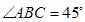 ,
, .
. ;
; 的正弦值;
的正弦值;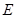 为棱
为棱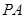 上的点,满足异面直线
上的点,满足异面直线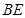 与
与 所成的角为
所成的角为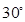 ,求
,求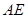 的长.
的长.
 中,
中, ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.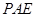 ;
;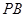 与平面
与平面
 ,
, 平面
平面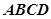 ,
,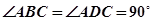 ,
, ,
,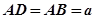 ,
, .
. 平面
平面 ;
; 到平面
到平面 的距离为
的距离为 时,求二面角
时,求二面角 的余弦值;
的余弦值; 为何值时,点
为何值时,点 内的射影
内的射影 恰好是
恰好是 的重心.
的重心.