题目内容
现有两个命题:(1)若lgx+lgy=lg(x+y),且不等式y>-2x+t恒成立,则t的取值范围是集合P;
(2)若函数
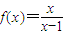 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;则以下集合关系正确的是( )
A.P?Q
B.Q?P
C.P=Q
D.P∩Q=∅
【答案】分析:由不等式y>-2x+t恒成立,即y+2x>t恒成立,转化为求y+2x的最小值即可;要使函数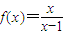 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,先考虑有交点时t的取值范围,再考虑其补集.
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,先考虑有交点时t的取值范围,再考虑其补集.
解答:解:由lgx+lgy=lg(x+y),得xy=x+y,两边同除以xy得 ,∴2x+y=(2x+y)
,∴2x+y=(2x+y)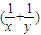 ═
═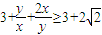 ,所以
,所以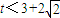 ;
;
又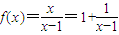 ,g(x)=-2x+t
,g(x)=-2x+t
由f(x)=g(x),得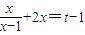 ,即
,即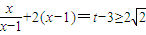 ,
,
∴函数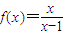 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点时t的取值范围时
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点时t的取值范围时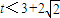
故选C.
点评:本题主要考查恒成立问题.利用基本不等式求最值,考查等价转化能力.
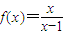 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,先考虑有交点时t的取值范围,再考虑其补集.
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,先考虑有交点时t的取值范围,再考虑其补集.解答:解:由lgx+lgy=lg(x+y),得xy=x+y,两边同除以xy得
 ,∴2x+y=(2x+y)
,∴2x+y=(2x+y)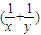 ═
═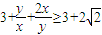 ,所以
,所以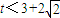 ;
;又
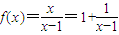 ,g(x)=-2x+t
,g(x)=-2x+t由f(x)=g(x),得
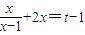 ,即
,即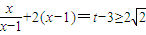 ,
,∴函数
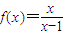 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点时t的取值范围时
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点时t的取值范围时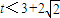
故选C.
点评:本题主要考查恒成立问题.利用基本不等式求最值,考查等价转化能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
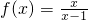 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;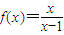 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;