题目内容
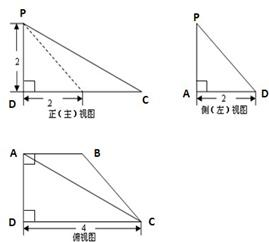 一个四棱锥P-ABCD的三视图如图所示.
一个四棱锥P-ABCD的三视图如图所示.(1)求四棱锥P-ABCD的体积;
(2)若E为CD中点,求证面PBD垂直于面PAE.
分析:(1)三视图复原几何体,是一条侧棱垂直底面直角梯形的时边的直角顶点,结合三视图的数据,直接求出几何体的体积.
(2)E为CD中点,如图,连接AE,BD,证明BD⊥平面PAE中的两条相交直线:PA,AE,即可证明面PBD垂直于面PAE.
(2)E为CD中点,如图,连接AE,BD,证明BD⊥平面PAE中的两条相交直线:PA,AE,即可证明面PBD垂直于面PAE.
解答:解:(1)三视图复原几何体,是一条侧棱垂直底面直角梯形的时边的直角顶点,
四棱锥的高为:2,底面直角梯形的底边为:4,高为:2,上底边长为:2,
所以四棱锥的体积为:
×
× 2×2=4.
(2)连接AE,BD,ABED是正方形,
所以BD⊥AE,PA⊥底面ABCD,BD?底面ABCD,
∴BD⊥PA,PA∩AE=A,BD⊥平面PAE,
∵BD?平面PBD,所以平面PBD⊥平面PAE.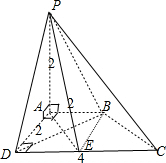
四棱锥的高为:2,底面直角梯形的底边为:4,高为:2,上底边长为:2,
所以四棱锥的体积为:
| 1 |
| 3 |
| (4+2) |
| 2 |
(2)连接AE,BD,ABED是正方形,
所以BD⊥AE,PA⊥底面ABCD,BD?底面ABCD,
∴BD⊥PA,PA∩AE=A,BD⊥平面PAE,
∵BD?平面PBD,所以平面PBD⊥平面PAE.

点评:本题考查三视图的复原,几何体的体积的求法,平面与平面垂直的证明,考查同学的空间想象能力,视图能力,计算能力,常考题型.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形,且四个顶点都在一个球面上,则该球的表面积为( )
A、
| ||
| B、2πa2 | ||
C、
| ||
| D、3πa2 |
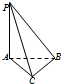 已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )
已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )