题目内容
若方程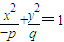 表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是( )
表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是( )A.
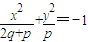
B.
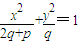
C.
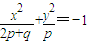
D.
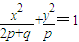
【答案】分析:若方程 表示双曲线则-pq<0即pq>0,①当p>0,q>0时,曲线
表示双曲线则-pq<0即pq>0,①当p>0,q>0时,曲线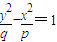 表示焦点在y轴的双曲线,②当p<0,q<0时,曲线
表示焦点在y轴的双曲线,②当p<0,q<0时,曲线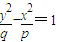 表示焦点在x轴的双曲线,结合选项可判定
表示焦点在x轴的双曲线,结合选项可判定
解答:解:若方程 表示双曲线则-pq<0即pq>0
表示双曲线则-pq<0即pq>0
①当p>0,q>0时,曲线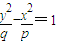 表示焦点在y轴的双曲线,
表示焦点在y轴的双曲线,
A,C的方程没有意义
B:由于2q+p>q>0,表示焦点在x轴上的椭圆,
D:由于2p+q>p>0,表示焦点在x轴上的椭圆
则此情况不符合题意,舍去
②当p<0,q<0时,曲线 表示焦点在x轴的双曲线
表示焦点在x轴的双曲线
A:由于-(2q+p)>-p>0,表示曲线是焦点在x轴上的椭圆
B:由于2q+p<q<0,方程没有意义
C:由于-2p-q>-p>0,表示焦点在x轴上上的椭圆
D:由于2p+q<p<0,方程没有意义
综合可得C对每种情况都符合题意
故选C
点评:本题主要考查了二次方程表示椭圆及双曲线的条件,及椭圆与双曲线的焦点位置的判定,属于基础方法应用的考查
 表示双曲线则-pq<0即pq>0,①当p>0,q>0时,曲线
表示双曲线则-pq<0即pq>0,①当p>0,q>0时,曲线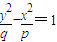 表示焦点在y轴的双曲线,②当p<0,q<0时,曲线
表示焦点在y轴的双曲线,②当p<0,q<0时,曲线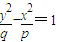 表示焦点在x轴的双曲线,结合选项可判定
表示焦点在x轴的双曲线,结合选项可判定解答:解:若方程
 表示双曲线则-pq<0即pq>0
表示双曲线则-pq<0即pq>0①当p>0,q>0时,曲线
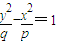 表示焦点在y轴的双曲线,
表示焦点在y轴的双曲线,A,C的方程没有意义
B:由于2q+p>q>0,表示焦点在x轴上的椭圆,
D:由于2p+q>p>0,表示焦点在x轴上的椭圆
则此情况不符合题意,舍去
②当p<0,q<0时,曲线
 表示焦点在x轴的双曲线
表示焦点在x轴的双曲线A:由于-(2q+p)>-p>0,表示曲线是焦点在x轴上的椭圆
B:由于2q+p<q<0,方程没有意义
C:由于-2p-q>-p>0,表示焦点在x轴上上的椭圆
D:由于2p+q<p<0,方程没有意义
综合可得C对每种情况都符合题意
故选C
点评:本题主要考查了二次方程表示椭圆及双曲线的条件,及椭圆与双曲线的焦点位置的判定,属于基础方法应用的考查

练习册系列答案
相关题目
 表示双曲线,则k的取值范围是( )
表示双曲线,则k的取值范围是( ) B.
B.
 D.
D. 或
或
 表示双曲线,则实数
表示双曲线,则实数  的取值范围是 ( )
的取值范围是 ( ) B.
B.

 D.
D. 
 表示双曲线,则实数k的取值范围是( )
表示双曲线,则实数k的取值范围是( ) 表示双曲线,则实数k的取值范围是
表示双曲线,则实数k的取值范围是 (B)
(B)
 或
或