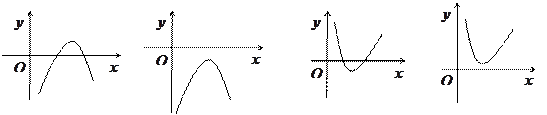题目内容
若奇函数f (x) (x∈R)满足f (2) = 1,f (x + 2) =" f" (x) + f (2),则f (1) =" ( " )
| A.0 | B.1 | C.-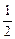 | D. |
D
解析

练习册系列答案
相关题目
函数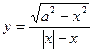 (a>0)的定义域是 ( )
(a>0)的定义域是 ( )
| A.[-a,a] | B.[-a,0]∪(0,a) |
| C.(0,a) | D.[-a,0] |
设定义在R上的函数f(x)满足f(x)f(x+2)=13,若f(1)=2,则f(99)="( " )
| A.13 | B.2 | C.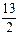 | D.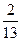 |
已知R上的奇函数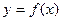 满足:
满足: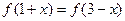 ,f(-2)=1,则
,f(-2)=1,则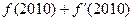 的值为 ( )
的值为 ( )
| A.2 | B.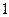 | C.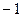 | D.-2 |
已知偶函数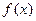 在区间
在区间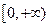 单调递增,则满足
单调递增,则满足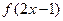 <
<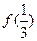 的x 取值范围是
的x 取值范围是
A.(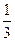 , , ) ) | B.(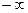 , , ) ) | C.(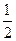 , , ) ) | D.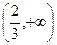 |
设函数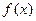 定义在实数集上,
定义在实数集上,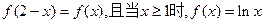 ,则有 ( )
,则有 ( )
A.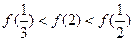 | B.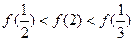 |
C.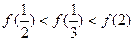 | D.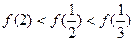 |
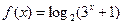 的值域为
的值域为
A. | B.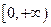 | C.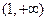 | D.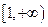 |
函数y=1+ln(x-1)(x>1)的反函数是
A.y=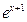 -1(x>0) -1(x>0) | B.y=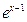 +1(x>0) +1(x>0) |
C.y=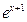 -1(x -1(x 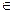 R) R) | D.y=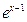 +1 (x +1 (x 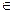 R) R) |
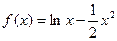 的图象大致是
的图象大致是