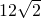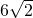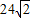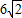题目内容
从抛物线y2=8x上一点P引其准线的垂线,垂足为M,设抛物线的焦点为F且|PF|=6,则△MPF的面积为( )
分析:根据抛物线定义结合PF的长可得|PM|=6,从而得到点P的横坐标为4,代入抛物线方程解出P的纵坐标,最后根据点P坐标和PM长,利用三角形面积公式即可算出△MPF的面积.
解答:解:设点P的坐标为(m,n),准线x=-2为直线l
∵PM⊥l,∴|PF|=|PM|=6
由此可得:m+2=6,解得m=4
∵P(m,n)是抛物线y2=8x上一点
∴n2=8×m=8×4=32,可得n=±4
因此,△MPF的面积为S=
|PM|•|n|=
×6×4
=12
故选:C

∵PM⊥l,∴|PF|=|PM|=6
由此可得:m+2=6,解得m=4
∵P(m,n)是抛物线y2=8x上一点
∴n2=8×m=8×4=32,可得n=±4
| 2 |
因此,△MPF的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选:C
点评:本题给出抛物线y2=8x上一点P到焦点F的距离为6,求该点的坐标并求△MPF的面积,着重考查了抛物线的定义与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
已知直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x的四个交点从上到下依次为A、B、C、D四点,则|AB|+|CD|=( )
| A、12 | B、14 | C、16 | D、18 |