题目内容
若实数x,y满足x2+y2+8x-6y+16=0,求x+y的最小值.
x+y的最小值为
.
解析:
原方程化为(x+4)2+(y-3)2=9,
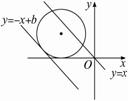
设x+y=b,则y=-x+b,
可见x+y的最小值就是过圆(x+4)2+(y-3)2=9上的点作斜率为-1的平行线中,纵截距b的最小值,此时,直线与圆相切.?
由点到直线的距离公式得
.
解得
或
.
所以x+y的最小值为.
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
解析:
孟建平小学滚动测试系列答案
B.10 C.9 D.5+2
B10
C9 D5＋2
<
.给出下列四个命题:①p∧q;?②p∨q;③
p;④
q.其中真命题的个数为( )