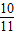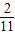题目内容
已知tan2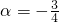 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)
,则tan(α+β)
- A.-2
- B.-1
- C.-

- D.-
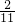
A
分析:根据α+β=2α-(α-β),利用两角差的正切公式,计算可得结论.
解答:∵α+β=2α-(α-β),tan2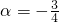 ,tan(α-β)=
,tan(α-β)= ,
,
∴tan(α+β)=tan[2α-(α-β)]=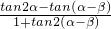 =
= =-2
=-2
故选A.
点评:本题考查两角差的正切公式的运用,考查学生的计算能力,解题的关键是利用α+β=2α-(α-β).
分析:根据α+β=2α-(α-β),利用两角差的正切公式,计算可得结论.
解答:∵α+β=2α-(α-β),tan2
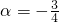 ,tan(α-β)=
,tan(α-β)= ,
,∴tan(α+β)=tan[2α-(α-β)]=
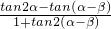 =
= =-2
=-2故选A.
点评:本题考查两角差的正切公式的运用,考查学生的计算能力,解题的关键是利用α+β=2α-(α-β).

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
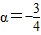 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)( )
,则tan(α+β)( )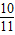
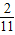
 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)= .
,则tan(α+β)= .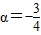 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)( )
,则tan(α+β)( )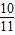
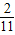
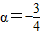 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)( )
,则tan(α+β)( )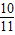
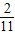
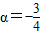 ,tan(α-β)=
,tan(α-β)= ,则tan(α+β)( )
,则tan(α+β)( )