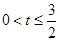题目内容
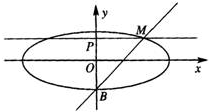
 如图,已知点B是椭圆
如图,已知点B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| BP |
| BM |
分析:由题意可得直线MB的方程为y=x-b,联立直线与椭圆方程可求M,由PM∥x轴可求P,结合已知及向量的数量积的定义,|
||
|cos45°=9可得|
|=3,从而可得t=3-b=
,整理可得a2=
,由t=3-b<b,a>b可求t的范围
. |
| BP |
. |
| BM |
. |
| BP |
| b(a2-b2) |
| b2+a2 |
| 3b2 |
| 2b-3 |
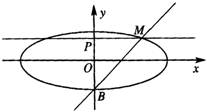
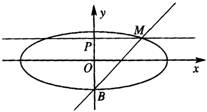
解答:解:由题意可得B(0,-b)
∴直线MB的方程为y=x-b
联立方程
可得(a2+b2)x2-2ba2x=0
∴M(
,
),
∵PM∥x轴
∴P(0,
)
∴
=(0,
+b),
=(
,
+b)
∵
•
=9,
由向量的数量积的定义可知,|
||
|cos45°=9
即|
|=3
∵P(0,t),B(0,-b)
∴t=3-b=
∴2a2b=3a2+3b2即a2=
∵t=3-b<b
∴b>
,t<
由a>b得a2=
>b2
∴b<3
∴t>0
综上所述0<t<
故选C
∴直线MB的方程为y=x-b
联立方程
|
∴M(
| 2ba2 |
| a2+b2 |
| b(a2-b2) |
| a2+b2 |
∵PM∥x轴
∴P(0,
| b(a2-b2) |
| a2+b2 |
∴
. |
| BP |
| b(a2-b2) |
| a2+b2 |
. |
| BM |
| 2ba2 |
| a2+b2 |
| b(a2-b2) |
| a2+b2 |
∵
| BP |
| BM |
由向量的数量积的定义可知,|
. |
| BP |
. |
| BM |
即|
. |
| BP |
∵P(0,t),B(0,-b)
∴t=3-b=
| b(a2-b2) |
| b2+a2 |
∴2a2b=3a2+3b2即a2=
| 3b2 |
| 2b-3 |
∵t=3-b<b
∴b>
| 3 |
| 2 |
| 3 |
| 2 |
由a>b得a2=
| 3b2 |
| 2b-3 |
∴b<3
∴t>0
综上所述0<t<
| 3 |
| 2 |
故选C
点评:本题主要考查了直线与椭圆的相交关系的应用,向量的基本运算的应用及一定的逻辑推理与运算的能力.

练习册系列答案
相关题目
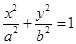
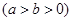 的短轴位于x轴下方的端点,
的短轴位于x轴下方的端点,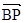 ?
? 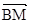 =9,若点P的坐标为(0,t),则t的取值范围是 ( )
=9,若点P的坐标为(0,t),则t的取值范围是 ( )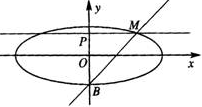
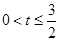

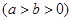 的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,
的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴, ,若点P的坐标为(0,t),则t的取值范围是
( )
,若点P的坐标为(0,t),则t的取值范围是
( )
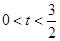 D.
D.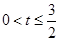
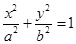
 的短轴位于x轴下方的端点,
的短轴位于x轴下方的端点, ,若点P的坐标为(0,t),则t的取值范围是
( )
,若点P的坐标为(0,t),则t的取值范围是
( )
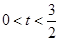 D.
D.