题目内容
看下面的问题:1+2+3+4+…+( )>10 000
这个问题的答案虽然不唯一,我们只要定出满足条件的最小正整数n0,括号内填写的数字只要大于或等于n0即可,试写出寻找满足条件的最小正整数n0的算法并画出相应的算法流程图.
解析:算法一:?
第一步:P=0;?
第二步:i=0;?
第三步:i=i+1;?
第四步:P=P+i;?
第五步:如果P>10 000,则输出i,否则,执行第六步;?
第六步:回到第三步,重新执行第三步,第四步,第五步.?
该算法的程序框图如下:?

算法二:?
第一步:取n的值等于1;?
第二步:计算n(n+1)2;?
第三步:如果n(n+1)2值大于10 000,那么n即为所求,否则,让n的值增加1,后转到第二步重复操作.?
该算法的流程图如下:?
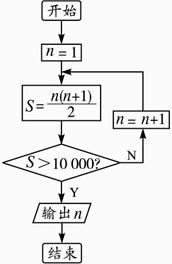
点评:由于10 000是一个较大的数,用试或猜的办法行不通,算法一是应用累加并循环的思路,算法二是应用公式并采用循环.如果对于算法二n的初始值是一个较大的数,如n=9 990,显然1+2+3+…+9 990>10 000.算法又应如何设计?请同学们自行解决.

练习册系列答案
相关题目