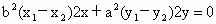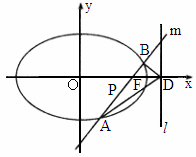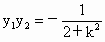题目内容
(2006
江西,21)如图所示,椭圆 (a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
(1)
求点P的轨迹H的方程;(2)
若在Q的方程中,令 ,
, .确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,△ABD的面积最大?
.确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,△ABD的面积最大?

答案:略
解析:
解析:
|
解析: (1)设椭圆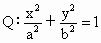 上的点 上的点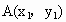 、 、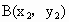 ,又设P点坐标为P(x,y), ,又设P点坐标为P(x,y),
则 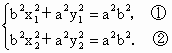
(i) 当AB不垂直x轴时,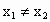 , ,
由①-②得
∴ 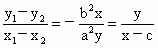 , ,
∴ 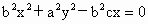 (*) (*)
(ii) 当AB垂直于x轴时,点P即为点F,满足方程(*),故所求点 P的轨迹H的方程为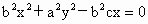 . .
(2) 因为椭圆Q右准线l方程是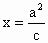 ,原点距椭圆Q的右准线l的距离为 ,原点距椭圆Q的右准线l的距离为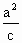 ,由于 ,由于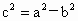 , ,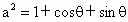 , ,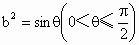 . .
则 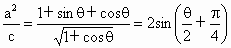 . .
当  时,上式达到最大值,所以当 时,上式达到最大值,所以当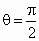 时,原点距椭圆Q的右准线l最远.此时 时,原点距椭圆Q的右准线l最远.此时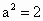 , ,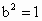 ,c=1,D(2,0),|DF|=1. ,c=1,D(2,0),|DF|=1.
设椭圆 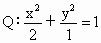 上的点 上的点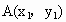 、 、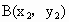 , ,
△ ABD面积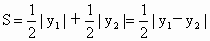 . .
设直线 m的方程为x=ky+1,代入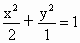 中, 中,
得 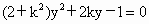 . .
由韦达定理得 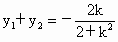 , ,
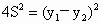 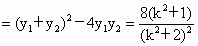 , ,
令 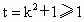 ,得 ,得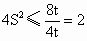 ,当t=1,即k=0时取等号. ,当t=1,即k=0时取等号.
因此,当直线 m绕点F转动到垂直x轴位置时,三角形ABD的面积最大. |

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目