题目内容
设x∈R,i是虚数单位,则“x=-3”是“复数z=(x2+2x-3)+(x-1)i为纯数”的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:由x=-3能得到复数z=(x2+2x-3)+(x-1)i为纯数,反之,复数z=(x2+2x-3)+(x-1)i为纯数得到x=-3,则答案可求.
解答:解:由x=-3,得x2+2x-3=(-3)2+2×(-3)-3=0,x-1=-3-1=-4.
而由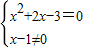 ,得x=-3.
,得x=-3.
所以“x=-3”是“复数z=(x2+2x-3)+(x-1)i为纯数”的充要条件.
故选C.
点评:本题考查了复数的基本概念,考查了必要条件、充分条件与充要条件的判断,复数为纯虚数的充要条件是不等于0且虚部不等于0,是基础题.
解答:解:由x=-3,得x2+2x-3=(-3)2+2×(-3)-3=0,x-1=-3-1=-4.
而由
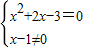 ,得x=-3.
,得x=-3.所以“x=-3”是“复数z=(x2+2x-3)+(x-1)i为纯数”的充要条件.
故选C.
点评:本题考查了复数的基本概念,考查了必要条件、充分条件与充要条件的判断,复数为纯虚数的充要条件是不等于0且虚部不等于0,是基础题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目