题目内容
(06年山东卷文)(12分)
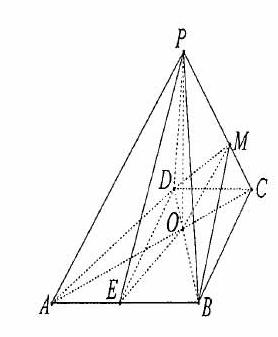
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直接PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且![]() 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.

解析:解法一:
![]() 平面
平面![]() ,
, ![]()
又![]() ,
,
由平面几何知识得:![]()
(Ⅰ)过![]() 做
做![]() 交于
交于![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() 或其补角为异面直线
或其补角为异面直线![]() 与
与![]() 所成的角,
所成的角,
![]() 四边形
四边形![]() 是等腰梯形,
是等腰梯形,![]()
![]()
又![]() ,
,![]() 四边形
四边形![]() 是平行四边形。
是平行四边形。
![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()
又![]() ,
,![]() 为直角三角形,
为直角三角形,
![]()
在![]() 中,由余弦定理得
中,由余弦定理得
![]()
故异面直线PD与![]() 所成的角的余弦值为
所成的角的余弦值为![]()
(Ⅱ)连结![]() ,由(Ⅰ)及三垂线定理知,
,由(Ⅰ)及三垂线定理知,![]() 为二面角
为二面角![]() 的平面角
的平面角
![]() ,
,![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]()
(Ⅲ)连结![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() ,又在
,又在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,故
,故![]() 时,
时,![]() 平面
平面![]()
解法二: ![]() 平面
平面![]() ,
,![]()
又![]() ,
,![]() ,
,
由平面几何知识得:![]()
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,

则各点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(Ⅰ)![]() ,
,![]() ,
,
![]() 。
。
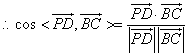
![]() 。
。
故直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]()
(Ⅱ)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由于![]() ,
,![]() ,
,
由 得
得 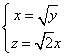
取![]() ,又已知平面ABCD的一个法向量
,又已知平面ABCD的一个法向量![]() ,
,
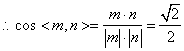
又二面角![]() 为锐角,
为锐角,
![]() 所求二面角
所求二面角![]() 的大小为
的大小为![]()
(Ⅲ)设![]() ,由于
,由于![]() 三点共线,
三点共线,![]() ,
,
![]() 平面
平面![]() ,
,
![]()
![]()
![]()
由(1)(2)知:![]() ,
,![]() 。
。
![]() ,
,![]()
故![]() 时,
时,![]() 平面
平面![]() 。
。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目