题目内容
已知椭圆C的中心在原点,焦点在x轴上,点F1、F2分别是椭圆的左、右焦点,在椭圆C的右准线上的点P(2,(1)求椭圆C的方程;
(2)若在椭圆C上存在点Q,满足![]() +
+![]() =λ
=λ![]() (O为坐标原点),求实数λ的取值范围;
(O为坐标原点),求实数λ的取值范围;
(3)在(2)的条件下,当λ取何值时,△ABO的面积最大,并求出这个最大值.
解:(1)设椭圆C的方程为![]() =1(a>b>0),半焦距为c,依题意有
=1(a>b>0),半焦距为c,依题意有
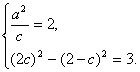 解得
解得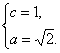 ∴b=1.
∴b=1.
∴所求椭圆方程为+y2=1.
(2)由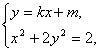 得(1+2k2)x2+4kmx+2m2-2=0.
得(1+2k2)x2+4kmx+2m2-2=0.
设点A、B的坐标分别为A(x1,y1)、B(x2,y2),
则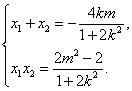 y1+y2=k(x1+x2)+2m=
y1+y2=k(x1+x2)+2m=![]() .
.
(ⅰ)当m=0时,点A、B关于原点对称,则λ=0.
(ⅱ)当m≠0时,点A、B不关于原点对称,则λ≠0,
由![]() +
+![]() =λ
=λ![]() ,得
,得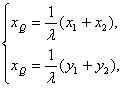 即
即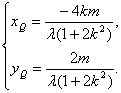 .
.
∵点Q在椭圆上,∴有[![]() ]2+2[
]2+2[![]() ]2=2.
]2=2.
化简,得4m2(1+2k2)=λ2(1+2k2)2.∵1+2k2≠0,∴有4m2=λ2(1+2k2).①
又∵Δ=16k2m2-4(1+2k2)(2m2-2)=8(1+2k2-m2),∴由Δ>0,得1+2k2>m2.②
由①②两式,得4m2>λ2m2.∵m≠0,∴λ2<4,则-2<λ<2且λ≠0.
综合(ⅰ)、(ⅱ)两种情况,得实数λ的取值范围是-2<λ<2.
(3)∵|AB|=![]() |x1-x2|,点O到直线AB的距离d=
|x1-x2|,点O到直线AB的距离d=![]() ,
,
∴△AOB的面积S=![]() |m||x1-x2|=
|m||x1-x2|=![]() |m|
|m|![]() =
=![]() .
.
由①有1+2k2=![]() ,代入上式并化简,得S=
,代入上式并化简,得S=![]()
![]() .
.
∵![]() ≤2,∴S≤
≤2,∴S≤![]() .
.
当且仅当λ2=4-λ2,即λ=±![]() 时,等号成立.
时,等号成立.
∴当λ=±2时,△ABO的面积最大,最大值为![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 。
。