题目内容
已知向量 ,
, .
.(1)若
 ,试判断
,试判断 与
与 能否平行?
能否平行?(2)若
 ,求函数
,求函数 的最小值.
的最小值.
【答案】分析:(1)若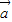 与
与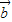 平行,则有
平行,则有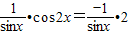 ,解得cos2x=-2,这与|cos2x|≤1相矛盾,故
,解得cos2x=-2,这与|cos2x|≤1相矛盾,故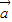 与
与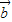 不能平行.
不能平行.
(2)化简函数的解析式为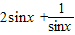 ,根据
,根据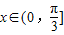 ,得
,得 ,利用基本不等式求出其最小值.
,利用基本不等式求出其最小值.
解答:解:(1)若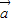 与
与 平行,则有
平行,则有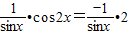 ,
,
因为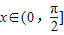 ,sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,故
,sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,故 与
与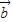 不能平行.
不能平行.
(2)由于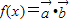 =
= ,
,
又因为 ,所以
,所以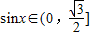 ,
,
于是 ,
,
当 ,即
,即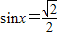 时取等号.
时取等号.
故函数f(x)的最小值等于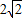 .
.
点评:本题考查两个向量共线的性质,两个向量的数量积公式,两个向量坐标形式的运算,基本不等式的应用,在利用基本不等式时,要注意检验等号成立的条件,这是解题的易错点.
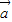 与
与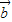 平行,则有
平行,则有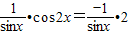 ,解得cos2x=-2,这与|cos2x|≤1相矛盾,故
,解得cos2x=-2,这与|cos2x|≤1相矛盾,故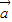 与
与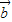 不能平行.
不能平行.(2)化简函数的解析式为
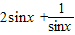 ,根据
,根据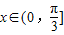 ,得
,得 ,利用基本不等式求出其最小值.
,利用基本不等式求出其最小值.解答:解:(1)若
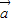 与
与 平行,则有
平行,则有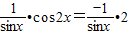 ,
,因为
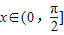 ,sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,故
,sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,故 与
与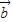 不能平行.
不能平行.(2)由于
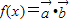 =
= ,
,又因为
 ,所以
,所以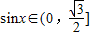 ,
,于是
 ,
,当
 ,即
,即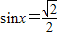 时取等号.
时取等号.故函数f(x)的最小值等于
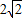 .
.点评:本题考查两个向量共线的性质,两个向量的数量积公式,两个向量坐标形式的运算,基本不等式的应用,在利用基本不等式时,要注意检验等号成立的条件,这是解题的易错点.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 ,
, .
. ,试判断
,试判断 与
与 能否平行?
能否平行? ,求函数
,求函数 的最小值.
的最小值. n=
n= .
. 的值;
的值; 中,角A,B,C的对边分别是a,b,c,且满足
中,角A,B,C的对边分别是a,b,c,且满足 求f(A)的取值范围.
求f(A)的取值范围.