题目内容

在a和b两数之间插入n个数，使他们与a，b组成等差数列，则该数列的公差为
b-a
n+1
b-a
n+1
．
分析：在a和b两个数之间插入n个数，使它们与a、b组成等差数列，说明这组等差数列中共有n+2个数，设出公差，运用等差数列通项公式求公差．
解答：解：由题意可得等差数列a1=a，an+2=b，
设其公差为d，则有an+2=a1+（n+2-1）d
即b=a+（n+1）d，解得d=
b-a
n+1

故答案为：
b-a
n+1
点评：本题考查等差数列的通项公式，解答此题的关键是明确总项数，属基础题．
练习册系列答案
相关题目
已知a，b是不相等的两个正数，在a，b之间插入两组数：x1，x2，…，xn和y1，y2，…，yn，（ n∈N*，且n≥2），使得a，x1，x2，…，xn，b成等差数列，a，y1，y2，…，yn，b成等比数列．老师给出下列五个式子：①
n
k=1
xk=
n(a+b)
2
；②
1
n
n
k=1
xk＞
ab
+(
a
-
b
2
)2；③
ny1y2…yn
＜
ab
；④
ny1y2…yn
=
ab
；⑤
ny1y2…yn
＞
ab
．其中一定成立的是
 
．
已知a、b是不相等的两个正数，在a、b之间插入两组数x1，x2，…xn和y1，y2，…yn（n∈N﹢，且n≥2），使得a，x1，x2，…xn，b成等差数列，a，y1，y2，…yn，b成等比数列，则下列四个式子中，一定成立的是
①②
①②
．（填上你认为正确的所有式子的序号）
①
n
k=i
xi=
n(a+b)
2
；②
1
n
n
k=i
xi=
a+b
2
＞
ab
+(
a
-
b
2
)2；③
ny1y2…yn
=
ab
；④
ny1y2…yn
＞
2ab
a+b
．

在a和b两数之间插入n个数，使它们与a，b组成等差数列，则该数列的公差为

[　　]

A．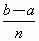

B．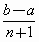

C．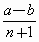

D．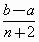
在7和56之间插入a,b两数,使7,a,b,56成等差数列,插入c,d两数,使7,c,d,56成等比数列,则a+b+c+d=____________________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网