题目内容
A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,且x+y+z=6),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.(1)用x、y、z表示B胜的概率;(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
(3)若规定A取红球,白球,黄球而获胜的得分分别为1,2,3分,否则得0分,求A得分的期望的最大值及此时x,y,z的值.
【答案】分析:(1)A胜与B胜为对立事件,A胜分为三个基本事件:①A1:“A、B均取红球”;②A2:“A、B均取白球”;③A3:“A、B均取黄球”.由此能求出用x、y、z表示B胜的概率.
(2)由(1)知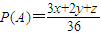 ,又x+y+z=6,x≥0,y≥0,z≥0,于是
,又x+y+z=6,x≥0,y≥0,z≥0,于是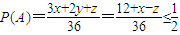 ,由此能求出A在箱中只放6个红球时,获胜概率最大,其值为
,由此能求出A在箱中只放6个红球时,获胜概率最大,其值为 .
.
(3)设A的得分为随机变量ξ,则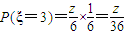 ;
;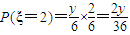 ;
;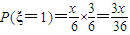 ;
;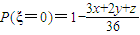 ,由此能求出A得分的期望的最大值及此时x,y,z的值.
,由此能求出A得分的期望的最大值及此时x,y,z的值.
解答:解:(1)显然A胜与B胜为对立事件,
A胜分为三个基本事件:
①A1:“A、B均取红球”;
②A2:“A、B均取白球”;
③A3:“A、B均取黄球”.
∵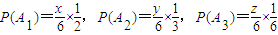
∴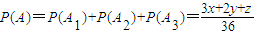 ,
,
∴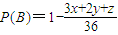
(2)由(1)知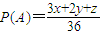 ,
,
又x+y+z=6,x≥0,y≥0,z≥0,
于是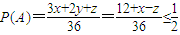 ,
,
∴当x=6,y=z=0,
即A在箱中只放6个红球时,获胜概率最大,其值为 .
.
(3)设A的得分为随机变量ξ,
则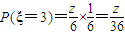 ;
;
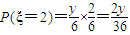 ;
;
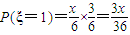 ;
;
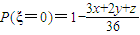 ,
,
∴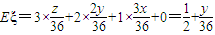 ,
,
∵x+y+z=6(x,y,z∈N),
∴y=6时,
Eξ取得最大值为 ,
,
此时x=z=0.
点评:本题考查概率在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意概率性质和古典概型的特征的灵活运用.
(2)由(1)知
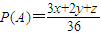 ,又x+y+z=6,x≥0,y≥0,z≥0,于是
,又x+y+z=6,x≥0,y≥0,z≥0,于是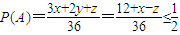 ,由此能求出A在箱中只放6个红球时,获胜概率最大,其值为
,由此能求出A在箱中只放6个红球时,获胜概率最大,其值为 .
.(3)设A的得分为随机变量ξ,则
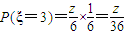 ;
;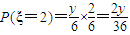 ;
;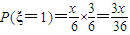 ;
;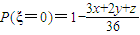 ,由此能求出A得分的期望的最大值及此时x,y,z的值.
,由此能求出A得分的期望的最大值及此时x,y,z的值.解答:解:(1)显然A胜与B胜为对立事件,
A胜分为三个基本事件:
①A1:“A、B均取红球”;
②A2:“A、B均取白球”;
③A3:“A、B均取黄球”.
∵
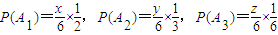
∴
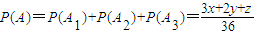 ,
,∴
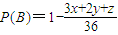
(2)由(1)知
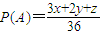 ,
,又x+y+z=6,x≥0,y≥0,z≥0,
于是
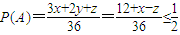 ,
,∴当x=6,y=z=0,
即A在箱中只放6个红球时,获胜概率最大,其值为
 .
.(3)设A的得分为随机变量ξ,
则
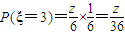 ;
;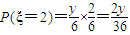 ;
;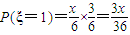 ;
;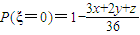 ,
,∴
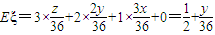 ,
,∵x+y+z=6(x,y,z∈N),
∴y=6时,
Eξ取得最大值为
 ,
,此时x=z=0.
点评:本题考查概率在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意概率性质和古典概型的特征的灵活运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目