题目内容
本小题满分10分)已知两直线l1:ax-by+4=0和l2:(a-1)x+y+b=0.若l1∥l2且坐标原点到两直线的距离相等,求a、b的值.
 或
或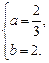
法一:∵l1∥l2且l2的斜率为1-a,
∴l1的斜率也存在,其值 =1-a.
=1-a.
∵1-a与a不可能同时为0,∴b= . ①
. ①
由原点到l1和l2的距离相等得
 =
= . ②
. ②
由①和②得 或
或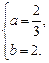
对于这两种情形,经检验知l1与l2都不重合.
∴ 或
或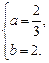
法二:两直线斜率都存在,化为斜截式得
l1:y= x+
x+ ,
,
l2:y=(1-a)x-b.
据题意作图,由直角三角形全等得两直线在y轴上的截距相反.

∴
解得 或
或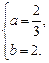
法三:据题意知,l1关于原点的中心对称图形是l2.
∴对l1:ax-by+4=0以-x代x且以-y代y得
l2:-ax+by+4=0.
又知l2:(a-1)x+y+b=0,
由两直线重合的条件得 =
= =
= .
.
解得 或
或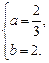
∴l1的斜率也存在,其值
 =1-a.
=1-a.∵1-a与a不可能同时为0,∴b=
 . ①
. ①由原点到l1和l2的距离相等得
 =
= . ②
. ②由①和②得
 或
或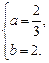
对于这两种情形,经检验知l1与l2都不重合.
∴
 或
或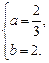
法二:两直线斜率都存在,化为斜截式得
l1:y=
 x+
x+ ,
,l2:y=(1-a)x-b.
据题意作图,由直角三角形全等得两直线在y轴上的截距相反.

∴

解得
 或
或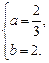
法三:据题意知,l1关于原点的中心对称图形是l2.
∴对l1:ax-by+4=0以-x代x且以-y代y得
l2:-ax+by+4=0.
又知l2:(a-1)x+y+b=0,
由两直线重合的条件得
 =
= =
= .
.解得
 或
或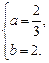

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 经过的象限是 ( )
经过的象限是 ( )

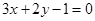

 和点
和点 的距离均为5的直线共有 ( )
的距离均为5的直线共有 ( ) 相切的直线方程是________
相切的直线方程是________ 与圆
与圆 的交点个数为 。
的交点个数为 。  过直线
过直线 和
和 的交点;
的交点; 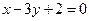 垂直,求直线
垂直,求直线 到直线
到直线 的距离为1.求直线
的距离为1.求直线 为法向量的直线过椭圆
为法向量的直线过椭圆 的右焦点,则该直线方程为
的右焦点,则该直线方程为  轴上的截距为
轴上的截距为 的直线方程是
的直线方程是


