题目内容
设 是等差数列,若
是等差数列,若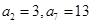 ,则数列
,则数列 前8项的和为( ).
前8项的和为( ).
| A.56 | B.64 | C.80 | D.128 |
B
解析试题分析:根据题意,由于 是等差数列,若
是等差数列,若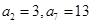 ,那么可知,5d=10.d=2,因此首项为1,那么可知数列的前8项的和为8+
,那么可知,5d=10.d=2,因此首项为1,那么可知数列的前8项的和为8+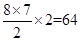 ,故可知答案为B.
,故可知答案为B.
考点:等差数列
点评:主要是考查了等差数列的通项公式以及求和公式的运用,属于基础题。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知等差数列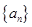 的公差
的公差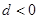 ,若
,若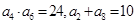 ,则该数列的前
,则该数列的前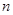 项和
项和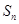 的最大值是( )
的最大值是( )
A.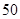 | B.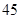 | C.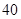 | D.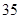 |
等差数列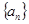 的前
的前 项和为
项和为 ,公差为
,公差为 ,已知
,已知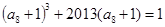 ,
,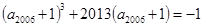 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B.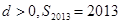 |
C.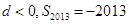 | D.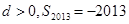 |
设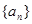 是等差数列,若
是等差数列,若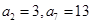 ,则数列
,则数列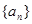 前8项的和为( )
前8项的和为( )
| A.128 | B.80 | C.64 | D.56 |
数列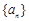 的前n项和为
的前n项和为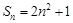 ,则an=( )
,则an=( )
| A.an=4n-2 |
| B.an=2n-1 |
C. |
D. |
等差数列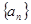 的公差
的公差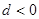 ,且
,且 ,则该数列的前
,则该数列的前 项和取得最大值时,
项和取得最大值时,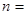
| A.6 | B.7 | C.6或7 | D.7或8 |
在数列 中,
中,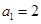 ,
,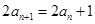 ,则
,则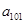 的值为 ( )
的值为 ( )
| A.49 | B.50 | C.51 | D.52 |
设等差数列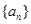 的前n项和为
的前n项和为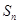 ,若
,若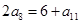 ,则
,则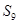 =( )
=( )
| A.54 | B.45 | C.36 | D.27 |
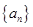 的前
的前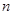 项和为
项和为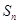 ,若
,若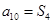 ,则
,则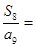 。
。