题目内容
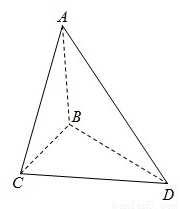
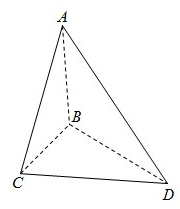 如图,AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC.
如图,AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC.(1)求AD与平面ABC所成的角的大小;
(2)若AB=2,求点B到平面ACD的距离.
分析:(1)因为AB⊥平面BCD,直线CD在平面BCD内,所以AB⊥CD且∠DAB是AD与平面BCD所成的角,则∠DAB=30°.又BC⊥CD,且AB.BC是平面ABC内的两条相交直线,所以CD⊥平面ABC,则∠DAC是AD与平面ABC所成的角.由此能求出AD与平面ABC所成的角.
(2)过B作BE⊥AC,交AC于E,由AB=BC=2,AB⊥BC,知E是AC的中点,由CD⊥平面ABC,知BE⊥CD,所以BE⊥面ACD,故点B到平面ACD的距离就是BE的长.
(2)过B作BE⊥AC,交AC于E,由AB=BC=2,AB⊥BC,知E是AC的中点,由CD⊥平面ABC,知BE⊥CD,所以BE⊥面ACD,故点B到平面ACD的距离就是BE的长.
解答:解:(1)∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD,且∠DAB是AD与平面BCD所成的角,
∴∠DAB=30°
∵BC⊥CD,AB∩BC=B,
∴CD⊥平面ABC,
∴∠DAC是AD与平面ABC所成的角.
在Rt△ABC中,AB=BC
由勾股定理得AC=
AB
在Rt△ABD中,
∵∠DAB=30°
∴AD=2AB
∴在Rt△ACD中,∠ACD=90°
cos∠DAC=
=
=
,
∴∠DAC=45°,
所以AD与平面ABC所成的角是45°.
(2)过B作BE⊥AC,交AC于E,
∵AB=BC=2,AB⊥BC,
∴E是AC的中点,
AC=2
,BE=
,
∵CD⊥平面ABC,
∴BE⊥CD,
∴BE⊥面ACD,
故点B到平面ACD的距离=BE=
.
∴AB⊥CD,且∠DAB是AD与平面BCD所成的角,
∴∠DAB=30°
∵BC⊥CD,AB∩BC=B,
∴CD⊥平面ABC,
∴∠DAC是AD与平面ABC所成的角.
在Rt△ABC中,AB=BC
由勾股定理得AC=
| 2 |
在Rt△ABD中,
∵∠DAB=30°
∴AD=2AB
∴在Rt△ACD中,∠ACD=90°
cos∠DAC=
| AC |
| AD |
| ||
| 2AB |
| ||
| 2 |
∴∠DAC=45°,
所以AD与平面ABC所成的角是45°.
(2)过B作BE⊥AC,交AC于E,
∵AB=BC=2,AB⊥BC,
∴E是AC的中点,
AC=2
| 2 |
| 2 |
∵CD⊥平面ABC,
∴BE⊥CD,
∴BE⊥面ACD,
故点B到平面ACD的距离=BE=
| 2 |
点评:本题考查直线与平面所成角的大小的求法和点到平面的距离的计算,解题时要认真审题,仔细解答,注意把空间问题等价转化为平面问题.本题的易错点是空间感差,不能正确地把空间几何问题转化为平面几何问题.

练习册系列答案
相关题目
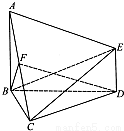
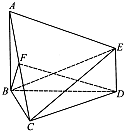 如图,AB⊥平面BCD,AB=BC=BD=2,DE∥AB,DE=1,∠CBD=60°,F为AC的中点.
如图,AB⊥平面BCD,AB=BC=BD=2,DE∥AB,DE=1,∠CBD=60°,F为AC的中点.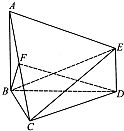 如图,AB⊥平面BCD,AB=BC=BD=2,DE∥AB,DE=1,∠CBD=60°,F为AC的中点.
如图,AB⊥平面BCD,AB=BC=BD=2,DE∥AB,DE=1,∠CBD=60°,F为AC的中点.