题目内容
已知{an}是各项都为正数的数列,其前n项和为Sn,且满足2anSn-an2=1.
(Ⅰ)求a1,a2,a3的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)令Tn=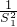 +
+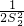 +…+
+…+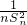 ,求证Tn≤
,求证Tn≤ .
.
解:(Ⅰ)令n=1则有2a21-a21=1,?a1=1(a1=-1舍去).
令n=2,得2(a1+a2)a2-a22=1,即a22+2a2-1=0.
∴ (舍去负值).
(舍去负值).
同理,令n=3可解得 .(3分)
.(3分)
(Ⅱ)∵2snan-an=1,①
又n≥2时有an=sn-sn-1,代入①式并整理得sn2-sn-12=1.
∴sn2是首项为1,公差为1的等差数列.(6分)
∴sn2=1+n-1=n,∴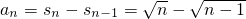 (n≥2),又a1=1
(n≥2),又a1=1
∴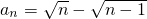 .(8分)
.(8分)
(Ⅲ)由(Ⅱ)知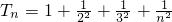 ≤1+
≤1+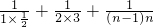
=1+1-1+(1 )+(
)+( )+(
)+(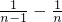 )=2-
)=2- =
=
即 .(12分)
.(12分)
分析:(Ⅰ)令n=1,导出a1=1.令n=2,导出 .令n=3可解得
.令n=3可解得 .
.
(Ⅱ)由2snan-an=1,an=sn-sn-1,知sn2-sn-12=1,所以s2n=1+n-1=n,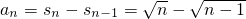 .
.
(Ⅲ)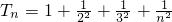 ≤1+
≤1+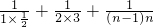 =1+1-1+(1
=1+1-1+(1 )+(
)+( )+(
)+(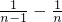 )=2-
)=2- =
= .
.
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.
令n=2,得2(a1+a2)a2-a22=1,即a22+2a2-1=0.
∴
 (舍去负值).
(舍去负值).同理,令n=3可解得
 .(3分)
.(3分)(Ⅱ)∵2snan-an=1,①
又n≥2时有an=sn-sn-1,代入①式并整理得sn2-sn-12=1.
∴sn2是首项为1,公差为1的等差数列.(6分)
∴sn2=1+n-1=n,∴
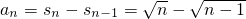 (n≥2),又a1=1
(n≥2),又a1=1∴
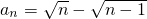 .(8分)
.(8分)(Ⅲ)由(Ⅱ)知
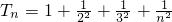 ≤1+
≤1+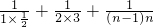
=1+1-1+(1
 )+(
)+( )+(
)+(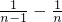 )=2-
)=2- =
=
即
 .(12分)
.(12分)分析:(Ⅰ)令n=1,导出a1=1.令n=2,导出
 .令n=3可解得
.令n=3可解得 .
.(Ⅱ)由2snan-an=1,an=sn-sn-1,知sn2-sn-12=1,所以s2n=1+n-1=n,
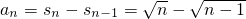 .
.(Ⅲ)
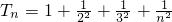 ≤1+
≤1+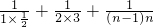 =1+1-1+(1
=1+1-1+(1 )+(
)+( )+(
)+(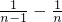 )=2-
)=2- =
= .
.点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 的前n项和.
的前n项和.