题目内容
设命题p: 是三个非零向量;命题q:
是三个非零向量;命题q: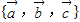 为空间的一组基,则命题q是命题p的( )
为空间的一组基,则命题q是命题p的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既非充分又非必要条件
【答案】分析:根据空间的一组基底满足的条件:不共面及零向量与任意向量关系的性质,判断出前者成立推不出后者成立;后者成立推出前者成立,利用充要条件的有关定义得到结论.
解答:解: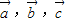 是三个非零向量成立,当
是三个非零向量成立,当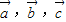 三个向量共面时,则
三个向量共面时,则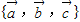 不为空间的一组基,
不为空间的一组基,
即命题p推不出命题q;
但反之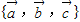 为空间的一组基,则
为空间的一组基,则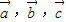 不共面,所以
不共面,所以 是三个非零向量,
是三个非零向量,
即命题q推出命题p;
所以命题q是命题p的充分不必要条件.
故选A.
点评:解决一个命题是另一个命题的什么条件,应该先确定哪一个是条件,再两边试着双推一下,利用充要条件的有关定义下结论.
解答:解:
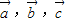 是三个非零向量成立,当
是三个非零向量成立,当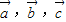 三个向量共面时,则
三个向量共面时,则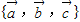 不为空间的一组基,
不为空间的一组基,即命题p推不出命题q;
但反之
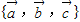 为空间的一组基,则
为空间的一组基,则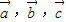 不共面,所以
不共面,所以 是三个非零向量,
是三个非零向量,即命题q推出命题p;
所以命题q是命题p的充分不必要条件.
故选A.
点评:解决一个命题是另一个命题的什么条件,应该先确定哪一个是条件,再两边试着双推一下,利用充要条件的有关定义下结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
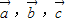 是三个非零向量;命题q:
是三个非零向量;命题q: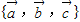 为空间的一组基,则命题q是命题p的( )
为空间的一组基,则命题q是命题p的( )